Vector axiomatics
vector point axiomatics
The axiomatics of an  -dimensional affine space
-dimensional affine space  , the basic concepts of which are "point" and "vector" ; the connection between them is realized by establishing a correspondence between a pair of points and a uniquely defined vector. The following axioms are valid.
, the basic concepts of which are "point" and "vector" ; the connection between them is realized by establishing a correspondence between a pair of points and a uniquely defined vector. The following axioms are valid.
I) The set of all vectors of 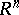 is an
is an  -dimensional vector space
-dimensional vector space  .
.
II) Any two points 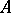 and
and 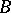 , given in a definite order, define a unique vector
, given in a definite order, define a unique vector 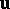 .
.
III) If a vector 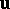 and a point
and a point  are arbitrary given, there exists only one point
are arbitrary given, there exists only one point 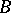 such that
such that 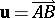 .
.
IV) If 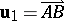 and
and 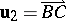 , then
, then 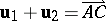 .
.
The pair "point A and vector u" is called "the vector u applied at the point A" (or "fixed at that point" ); the point 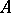 itself is said to be the origin of the vector
itself is said to be the origin of the vector  applied at it, while the point
applied at it, while the point 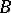 which is uniquely defined by the pair
which is uniquely defined by the pair 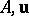 is said to be the end of the vector
is said to be the end of the vector 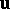 (applied at
(applied at  ).
).
An arbitrarily given vector 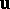 generates a completely defined one-to-one mapping of the set of all points of
generates a completely defined one-to-one mapping of the set of all points of 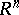 onto itself. This mapping, which is known as the translation of
onto itself. This mapping, which is known as the translation of  over the vector
over the vector 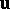 , relates each point
, relates each point 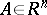 to the end
to the end 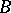 of the vector
of the vector 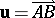 .
.
References
| [1] | P.S. Aleksandrov, "Lectures on analytical geometry" , Moscow (1968) (In Russian) |
| [2] | P.S. Alexandroff [P.S. Aleksandrov] (ed.) et al. (ed.) , Enzyklopaedie der Elementarmathematik , 4. Geometrie , Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian) |
Comments
Cf. also (the editorial comments to) Vector or [a1].
References
| [a1] | M. Berger, "Geometry" , I , Springer (1987) pp. Chapt. 2 |
Vector axiomatics. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vector_axiomatics&oldid=49134