Variation of a mapping
A numerical characteristic of a mapping connected with its differentiability properties. Defined by S. Banach [1]. The definition given below applies to the two-dimensional case only. Consider the mapping
 |
where  and
and  are continuous functions on the square
are continuous functions on the square  . One says that the mapping
. One says that the mapping  is of bounded variation if there exists a number
is of bounded variation if there exists a number  such that for any sequences non-intersecting squares
such that for any sequences non-intersecting squares  (
( ), with sides parallel to the coordinate axes
), with sides parallel to the coordinate axes  , the inequality
, the inequality
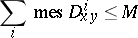 |
is true. Here 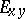 denotes the image of a set
denotes the image of a set 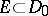 under the mapping
under the mapping 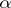 , and
, and  is the plane Lebesgue measure of
is the plane Lebesgue measure of  . The numerical value
. The numerical value  of the variation of
of the variation of 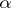 may be determined in various ways. For instance, let
may be determined in various ways. For instance, let 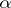 be of bounded variation. The variation
be of bounded variation. The variation  may then be determined by the formula
may then be determined by the formula
 |
where  is the number of solutions of the system
is the number of solutions of the system  ,
,  (the Banach indicatrix of
(the Banach indicatrix of  ).
).
If  is of bounded variation, then, almost-everywhere on
is of bounded variation, then, almost-everywhere on 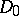 , the generalized Jacobian
, the generalized Jacobian  (
( ) exists, and it is integrable on
) exists, and it is integrable on  ; also,
; also,
 |
where  is a square containing the point
is a square containing the point  with sides parallel to the axes
with sides parallel to the axes 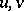 [2].
[2].
References
| [1] | S. Banach, "Sur les lignes rectifiables et les surfaces dont l'aire est finie" Fund. Math. , 7 (1925) pp. 225–236 |
| [2] | L.D. Kudryavtsev, "The variation of mappings in regions" , Metric questions in the theory of functions and mappings , 1 , Kiev (1969) pp. 34–108 (In Russian) |
Comments
References
| [a1] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
Variation of a mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Variation_of_a_mapping&oldid=49115