Vandermonde determinant

A determinant of order of the type

(*)

where are elements of a commutative ring. For any ,

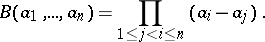If the ring has no zero divisors, the fundamental property of a Vandermonde determinant holds: 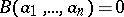if and only if not all the elements are different from each other. The determinant was first studied by A.T. Vandermonde for the case 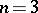, and then in 1815 by A.L. Cauchy .

References

[1a]	A.T. Vandermonde, Histoire Acad. R. Sci. Paris (1771 (1774)) pp. 365–416
[1b]	A.T. Vandermonde, Histoire Acad. R. Sci. Paris (1772 (1776)) pp. 516–532
[2a]	A.A. Cauchy, "Mémoire sur les fonctions qui ne peuvent obtenir que deux values" J. École Polytechnique , 17 : 10 (1815) pp. 29-
[2b]	A.L. Cauchy, "Mémoire sur les fonctions qui ne peuvent obtenir que deux values" , Oeuvres Sér. 2 , 1 , Gauthier-Villars (1905) pp. 91–169

Comments

The matrix

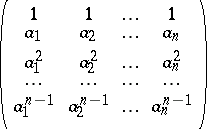participating in (*) is called a Vandermonde matrix.

The Vandermonde matrix plays a role in approximation theory. E.g., using it one can prove that there is a unique polynomial of degree taking prescribed values at 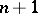distinct points, cf. [a1], p. 58. See [a1], p. 64, Problem 13, for an algorithm to compute the inverse of a Vandermonde matrix.

References

[a1]	E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982)