Urysohn equation
A non-linear integral equation of the form
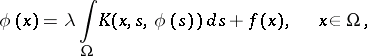 | (*) |
where  is a bounded closed set in a finite-dimensional Euclidean space and
is a bounded closed set in a finite-dimensional Euclidean space and 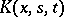 and
and 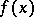 are given functions for
are given functions for 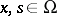 ,
,  . Suppose that
. Suppose that 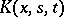 is continuous for the set of variables
is continuous for the set of variables  ,
, 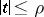 (where
(where 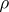 is some positive number), and let
is some positive number), and let
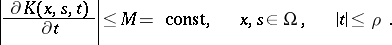 |
If
 |
 |
then the equation
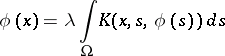 |
has a unique continuous solution  ,
,  , satisfying the inequality
, satisfying the inequality  . If
. If  is any continuous function satisfying
is any continuous function satisfying 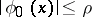 (
( ), then the sequence of approximations
), then the sequence of approximations
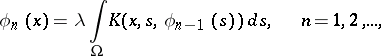 |
converges uniformly on  to
to  .
.
Let the Urysohn operator
 |
act in the space  ,
,  , and let for all
, and let for all  ,
,  the inequality
the inequality
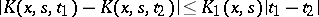 |
be fulfilled, where  is a measurable function satisfying
is a measurable function satisfying
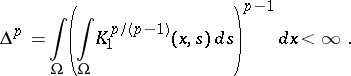 |
Then for  and
and  , equation (*) has a unique solution in
, equation (*) has a unique solution in  .
.
Under certain assumptions, equation (*) was first studied by P.S. Urysohn (cf. Non-linear integral equation).
References
| [1] | M.A. Krasnosel'skii, "Topological methods in the theory of nonlinear integral equations" , Pergamon (1964) (Translated from Russian) |
| [2] | P.P. Zabreiko (ed.) A.I. Koshelev (ed.) M.A. Krasnoselskii (ed.) S.G. Mikhlin (ed.) L.S. Rakovshchik (ed.) V.Ya. Stet'senko (ed.) T.O. Shaposhnikova (ed.) R.S. Anderssen (ed.) , Integral equations - a reference text , Noordhoff (1975) (Translated from Russian) |
Urysohn equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Urysohn_equation&oldid=49100