Unramified character

A character (cf. Character of a group) of the Galois group of a Galois extension of local fields that is trivial on the inertia subgroup. Any unramified character can be regarded as a character of the Galois group of the extension , where is the maximal unramified subfield of the extension . The unramified characters form a subgroup of the group of all characters. A character of the multiplicative group of a local field that is trivial on the group of units of is also called unramified. This definition is compatible with the preceding one, because by the fundamental theorem of local class field theory there is for every Abelian extension of local fields a canonical reciprocity homomorphism that enables one to identify the set of characters of the group 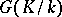with a certain subgroup of the character group of .

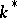For a Galois extension of global fields a character of the Galois group is said to be unramified at a point 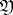of if it remains unramified in the above sense under restriction to the decomposition subgroup of any point 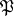of lying over 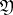. Similarly, a character of the idèle class group of 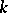is called unramified at if its restriction to the subgroup of units of the completion 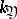of relative to 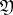is trivial, where the group is imbedded in the standard way in .

From global class field theory it follows that these two definitions of being unramified at a point are compatible, as in the local case.

References

[1]	A. Weil, "Basic number theory" , Springer (1974)

Comments

See Ramified prime ideal and Inertial prime number for the notion of inertia subgroup.