Universal normal algorithm

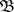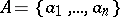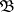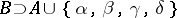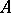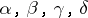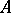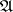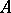A normal algorithm which in a sense (made precise below) models the work of any normal algorithm over the alphabet . A normal algorithm over the alphabet (where does not contain ) is called universal for if for every normal algorithm over and any word 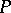over ,

Here is a representation of the normal algorithm (cf. Algorithm, representation of an), and the symbol 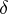in 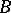plays the role of dividing sign. The existence of a universal normal algorithm was proved by A.A. Markov (cf. [1]). An important characteristic of a universal normal algorithm is its complexity, i.e. the length of its representation (cf. also Algorithm, complexity of description of an). A universal normal algorithm of minimal complexity as a function of (the number of symbols in the alphabet ) has been obtained, differing only by an additive constant from lower and upper bounds of the form 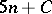(cf. [2]).

References

[1]	A.A. Markov, "Theory of algorithms" , Israel Program Sci. Transl. (1961) (Translated from Russian) (Also: Trudy Mat. Inst. Steklov. 42 (1954))
[2]	V.G. Zharov, "The complexity of a universal normal algorithm" , Theory of algorithms and mathematical logic , Moscow (1974) pp. 34–54 (In Russian)

References

[a1]	A.A. Markov, N.M. [N.M. Nagornyi] Nagorny, "The theory of algorithms" , Kluwer (1988) pp. Chapt. V (Translated from Russian)