Typically-real function

in a domain

A function 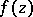, analytic in some domain in the -plane containing segments of the real axis, which is real on these segments and for which 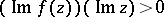whenever 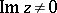. A fundamental class of typically-real functions is the class of functions

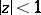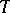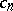that are regular and typically real in the disc (cf. [1]). It follows from the definition of the class that is real for 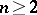. The class 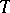contains the class of functions

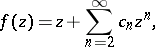with real coefficients 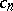, that are regular and univalent in 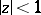(cf. Univalent function). If 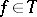, then

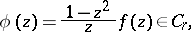and, conversely, if 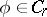, then

where 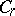is the class of functions

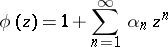that are regular in 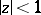with in 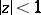and such that 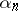is real for .

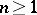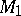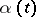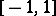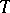Let be the class of non-decreasing functions on for which . Functions of class can be represented in 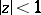by Stieltjes integrals (cf. [2]):

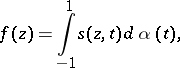(1)

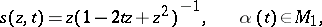in the sense that for each 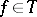there exists an 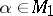such that (1) holds and, conversely, for any 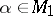formula (1) defines some function 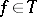. One has for any fixed 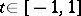. The largest domain in which every function in 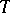is univalent is 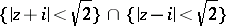. From the representation (1) for the class 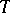, a number of rotation and distortion theorems have been obtained (cf. Distortion theorems; Rotation theorems). The following hold in the class :

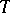(2)

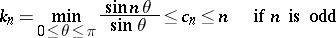(3)

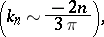with equality on the left in (2) only for 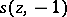and on the right only for 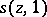, on the left in (3) only for functions 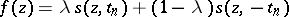for some 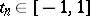, and on the right only for , .

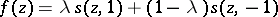For 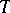, the coefficient regions for the systems 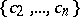, , , , 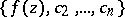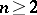have been found (cf. [3]).

References

[1]	W. Rogosinski, "Ueber positive harmonische Entwicklungen und typische-reelle Potenzreihen" Math. Z. , 35 (1932) pp. 93–121
[2]	G.M. Goluzin, "On typically real functions" Mat. Sb. , 27 : 2 (1950) pp. 201–218 (In Russian)
[3]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)

References

[a1]	P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11
[a2]	A.W. Goodman, "Univalent functions" , 1 , Mariner (1983)