Tube domain

tube

A domain 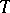in the complex space 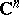of the form

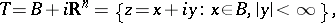where 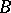is a domain in the real subspace 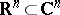, called the base of the tube domain 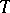. A domain of the form 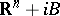is also called a tube domain. The holomorphic envelope of an arbitrary tube domain is the same as its convex hull; in particular, every function that is holomorphic in a tube domain 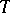can be extended to a function that is holomorphic in the convex hull of 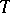. A tube domain is said to be radial if its base is a connected cone in .

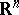References

[1]	V.S. Vladimirov, "Methods of the theory of functions of many complex variables" , M.I.T. (1966) (Translated from Russian)

References

[a1]	L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) pp. Chapt. 2.4