Triangulation
A triangulation of a polyhedron, or rectilinear triangulation, is a representation of the polyhedron (cf. Polyhedron, abstract) as the space of a geometric simplicial complex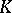 
, that is, a decomposition of it into closed simplices such that any two simplices either do not intersect or intersect along a common face. Rectilinear triangulations of polyhedra serve as the main tool for studying them. Any polyhedron has a triangulation and any two triangulations of it have a common subdivision.
The closed star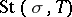 
of a simplex 
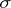in a triangulation 
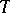is the union of the simplices of 
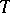containing 
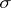. There is a representation of the closed star of a simplex 
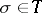as the union (or join, cf. Union of sets) of 
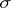and its link: 
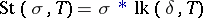. In particular, the star of a vertex is a cone over its link. If a simplex 
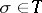is represented as the join of two of its faces 
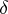and 
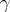, then 
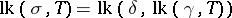. The link of a simplex does not depend on 
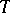: If 
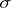is a simplex in rectilinear triangulations 
, 
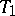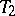of the same polyhedron, then the polyhedra 
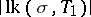and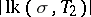 
are PL-homeomorphic. The open star of a simplex 
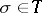is defined as the union of the interiors of those simplices of 
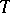containing 
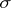as a face. The open stars of the vertices of a triangulation of a polyhedron 
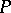form an open covering of 
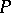. The nerve of this covering (cf. Nerve of a family of sets) is simplicially isomorphic to the triangulation. Two triangulations 
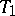and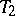 
of polyhedra 
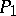and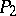 
are combinatorially equivalent if certain subdivisions of them are simplicially isomorphic. In order that two triangulations 
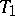and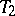 
be combinatorially equivalent it is necessary and sufficient that 
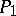and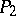 
be PL-homeomorphic. A triangulation of a manifold is said to be combinatorial if the star of any of its vertices is combinatorially equivalent to a simplex. In this case the star of any simplex of the triangulation is also combinatorially equivalent to a simplex.
If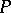 
is a closed subpolyhedron of a polyhedron 
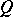, then any triangulation 
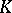of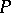 
can be extended to some triangulation 
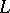of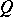 
. In this case one says that the pair of geometric simplicial complexes 
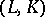triangulates the pair 
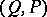. A triangulation of the direct product 
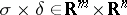of two simplices 
, 
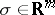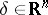can be constructed as follows. The vertices of the triangulation are the points 
, 
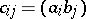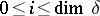, where 
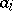are the vertices of 
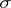and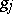 
are the vertices of 
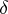. The vertices 
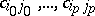, where 
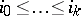, span a 
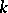-dimensional simplex if and only if none of these coincide and 
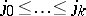. A triangulation of the direct product of two simplicial complexes with ordered vertices can be carried out in the same way.
A triangulation of a topological space, or curvilinear triangulation, is a pair 
, where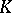 
is a geometric simplicial complex and 
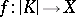is a homeomorphism. Two triangulations 
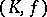and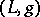 
of a space 
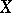coincide if 
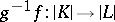is a simplicial isomorphism. If 
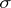is a simplex of a complex 
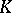and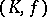 
is a triangulation of 
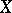, then the space 
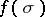endowed with the homeomorphism 
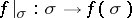is called a topological simplex. The star and the link of a topological simplex of a triangulated topological space are defined in the same way as in the case of rectilinear triangulations. If a point 
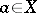is a vertex of triangulations 
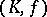and 
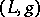of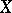 
, then its links in these triangulations are homotopy equivalent.
References
| [1] | P.S. Aleksandrov, "Combinatorial topology" , Graylock , Rochester (1956) (Translated from Russian) |
| [2] | D.B. Fuks, V.A. Rokhlin, "Beginner's course in topology. Geometric chapters" , Springer (1981) (Translated from Russian) |
Comments
References
| [a1] | E.C. Zeeman, "Seminar on combinatorial topology" , IHES (1963) |
| [a2] | H. Seifert, W. Threlfall, "Lehrbuch der Topologie" , Chelsea, reprint (1970) |
| [a3] | I.M. Singer, J.A. Thorpe, "Lecture notes on elementary topology and geometry" , Springer (1967) |
| [a4] | L.C. Glaser, "Geometrical combinatorial topology" , 1–2 , v. Nostrand (1970) |
Triangulation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Triangulation&oldid=49033