Translations of semi-groups
Transformations of semi-groups that satisfy special conditions: a right translation of a semi-group 
is a transformation 
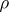such that 
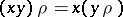for any 
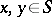; a left translation is defined similarly. For convenience, left translations are often written as left operators. Thus, a left translation of 
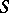is a transformation 
such that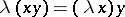 
for any 
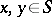. The successive application of two left translations (see Transformation semi-group) is written from right to left. The product of two left (respectively, right) translations of a semi-group is itself a left (respectively, right) translation, so that the set 
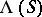(respectively, 
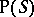) of all left (respectively, right) translations of 
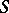is a sub-semi-group of the symmetric semi-group 
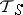. For any 
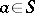the transformation 
(
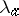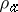) defined by 
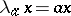(respectively, 
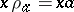) is the left (respectively, right) translation corresponding to 
. It is called the inner left (respectively, right) translation. The set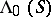 
(respectively, 
) of all inner left (respectively, right) translations of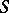 
is a left ideal in 
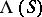(respectively, a right ideal in 
).
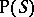A left translation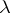 
and a right translation 
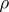of 
are called linked if 
for any 
; in this case the pair 
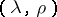is called a bi-translation of 
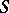. For any 
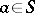, the pair 
is a bi-translation, called the inner bi-translation corresponding to 
. In semi-groups with a unit, and only in them, every bi-translation is inner. The set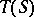 
of all bi-translations of 
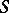is a sub-semi-group of the Cartesian product 
; it is called the translational hull of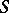 
. The set 
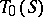of all inner bi-translations is an ideal in 
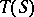, called the inner part of 
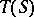. The mapping 
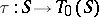defined by 
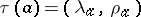is a homomorphism of 
onto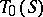 
, called the canonical homomorphism. A semi-group 
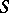is called weakly reductive if for any 
the relations 
and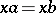 
for all 
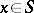imply that 
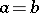, that is, the canonical homomorphism of 
is an isomorphism. If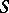 
is weakly reductive, then 
coincides with the idealizer of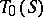 
in 
, that is, with the largest sub-semi-group of 
containing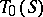 
as an ideal.
Translations of semi-groups, and in particular, translational hulls, play an important role in the study of ideal extensions of semi-groups (cf. Extension of a semi-group). Here the role of the translational hull is to a certain extent similar to that of the holomorph of a group in group theory.
References
| [1] | A.H. Clifford, G.B. Preston, "The algebraic theory of semi-groups" , 1 , Amer. Math. Soc. (1967) |
| [2] | M. Petrich, "Introduction to semigroups" , C.E. Merrill (1973) |
| [3] | M. Petrich, "The translational hull in semigroups and rings" Semigroup Forum , 1 (1970) pp. 283–360 |
Translations of semi-groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Translations_of_semi-groups&oldid=49018