Transcendental branch point
From Encyclopedia of Mathematics
of an analytic function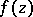 
A branch point that is not an algebraic branch point. In other words, it is either a branch point 
of finite order 
at which, however, there does not exist a finite or infinite limit
 |
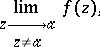or a logarithmic branch point of infinite order. For example, the first possibility is realized at the transcendental branch point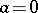 
for the function 
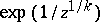, the second for the function 
.
In the first case the function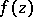 
can be expanded in a neighbourhood of 
in the form of a Puiseux series
 |
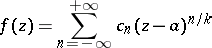with an infinite number of non-zero coefficients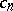 
with negative indices.
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) (Translated from Russian) |
How to Cite This Entry:
Transcendental branch point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transcendental_branch_point&oldid=49007
Transcendental branch point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transcendental_branch_point&oldid=49007
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article