Total increment
of a function of several variables
The increment acquired by the function when all the arguments undergo, in general non-zero, increments. More precisely, let a function 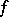 be defined in a neighbourhood of the point
be defined in a neighbourhood of the point 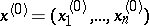 in the
in the  -dimensional space
-dimensional space 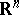 of the variables
of the variables  . The increment
. The increment
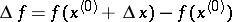 |
of the function 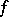 at
at 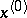 , where
, where
 |
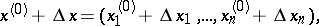 |
is called the total increment if it is considered as a function of the  possible increments
possible increments 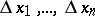 of the arguments
of the arguments  , which are subject only to the condition that the point
, which are subject only to the condition that the point 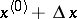 belongs to the domain of definition of
belongs to the domain of definition of  . Along with the total increment of the function, one can consider the partial increments
. Along with the total increment of the function, one can consider the partial increments 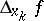 of
of 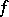 at a point
at a point 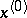 with respect to the variable
with respect to the variable 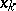 , i.e. increments
, i.e. increments 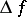 for which
for which 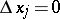 ,
, 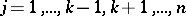 , and
, and 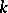 is fixed
is fixed 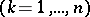 .
.
Total increment. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Total_increment&oldid=49002