Functions of the points on a torus that arise when solving the Laplace equation by the method of separation of variables (cf. Separation of variables, method of) in toroidal coordinates  . A harmonic function
. A harmonic function  , which is a solution of the Laplace equation, can be written as a series
, which is a solution of the Laplace equation, can be written as a series
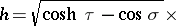 | (*) |
where the  ,
,  are the associated Legendre functions with half-integer index. By setting
are the associated Legendre functions with half-integer index. By setting  one obtains a toroidal harmonic or a surface toroidal harmonic, this in contrast with the expression (*) which, as a function of the three variables
one obtains a toroidal harmonic or a surface toroidal harmonic, this in contrast with the expression (*) which, as a function of the three variables  , is sometimes called a spatial toroidal harmonic.
, is sometimes called a spatial toroidal harmonic.
The series (*) is used in the solution of boundary value problems in toroidal coordinates, taking into account the expansion
where 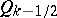 is the Legendre function of the second kind.
is the Legendre function of the second kind.
References
| [1] | A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [2] | P.M. Morse, H. Feshbach, "Methods of theoretical physics" , 1–2 , McGraw-Hill (1953) |
References
| [a1] | H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 1. The gamma function. The hypergeometric functions. Legendre functions , McGraw-Hill (1953) (Formula 3.10 (3)) |
How to Cite This Entry:
Toroidal harmonics. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Toroidal_harmonics&oldid=48997
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article . A harmonic function
. A harmonic function  , which is a solution of the Laplace equation, can be written as a series
, which is a solution of the Laplace equation, can be written as a series
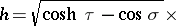
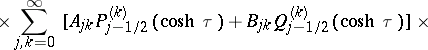
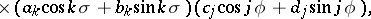
 ,
,  are the associated Legendre functions with half-integer index. By setting
are the associated Legendre functions with half-integer index. By setting  one obtains a toroidal harmonic or a surface toroidal harmonic, this in contrast with the expression (*) which, as a function of the three variables
one obtains a toroidal harmonic or a surface toroidal harmonic, this in contrast with the expression (*) which, as a function of the three variables  , is sometimes called a spatial toroidal harmonic.
, is sometimes called a spatial toroidal harmonic.
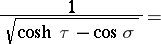
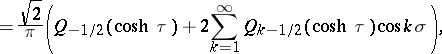
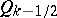 is the Legendre function of the second kind.
is the Legendre function of the second kind.