Topology of uniform convergence
The topology on the space 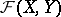 of mappings from a set
of mappings from a set 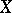 into a uniform space
into a uniform space 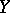 generated by the uniform structure on
generated by the uniform structure on 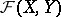 , the base for the entourages of which are the collections of all pairs
, the base for the entourages of which are the collections of all pairs 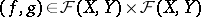 such that
such that 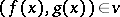 for all
for all 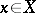 and where
and where  runs through a base of entourages for
runs through a base of entourages for 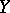 . The convergence of a directed set
. The convergence of a directed set 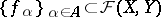 to
to 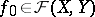 in this topology is called uniform convergence of
in this topology is called uniform convergence of 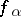 to
to 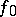 on
on 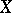 . If
. If 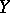 is complete, then
is complete, then 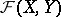 is complete in the topology of uniform convergence. If
is complete in the topology of uniform convergence. If 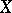 is a topological space and
is a topological space and 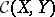 is the set of all mappings from
is the set of all mappings from 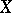 into
into 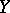 that are continuous, then
that are continuous, then 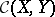 is closed in
is closed in 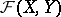 in the topology of uniform convergence; in particular, the limit
in the topology of uniform convergence; in particular, the limit 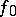 of a uniformly-convergent sequence
of a uniformly-convergent sequence 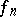 of continuous mappings on
of continuous mappings on 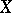 is a continuous mapping on
is a continuous mapping on  .
.
References
| [1] | N. Bourbaki, "General topology" , Elements of mathematics , Springer (1988) (Translated from French) |
| [2] | J.L. Kelley, "General topology" , Springer (1975) |
Comments
If 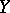 is a metric space with the uniform structure defined by the metric, then a basis for the open sets in
is a metric space with the uniform structure defined by the metric, then a basis for the open sets in 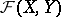 is formed by the sets
is formed by the sets 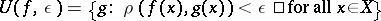 , and one finds the notion of uniform convergence in the form it is often encountered in e.g. analysis.
, and one finds the notion of uniform convergence in the form it is often encountered in e.g. analysis.
References
| [a1] | R. Engelking, "General topology" , Heldermann (1989) |
Topology of uniform convergence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Topology_of_uniform_convergence&oldid=48994