Topology of compact convergence

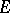One of the topologies on a space of continuous functions; the same as the compact-open topology. For the space of linear mappings from a locally convex space into a locally convex space 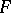, the topology of compact convergence is one of the 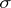-topologies, i.e. a topology of uniform convergence on sets belonging to a family 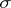of bounded sets in 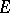; it is compatible with the vector space structure of and it is locally convex.

Comments

Thus, the topology of compact convergence on 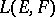is defined by the family of all compact sets, [a1].

The topology of pre-compact convergence is the 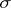-topology defined by the family of all pre-compact sets, [a2].

The topology of compact convergence in all derivatives in the space of all 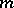times differentiable real- or complex-valued functions on 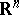is defined by the family of pseudo-norms

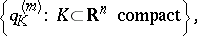The resulting space of functions is locally convex and metrizable, [a3].

References

[a1]	F. Trèves, "Topological vectorspaces, distributions and kernels" , Acad. Press (1967) pp. 198
[a2]	G. Köthe, "Topological vector spaces" , 1 , Springer (1969) pp. 263ff
[a3]	J.L. Kelley, I. Namioka, "Linear topological spaces" , v. Nostrand (1963) pp. 82