Tits bundle

The holomorphic fibration of a compact connected homogeneous complex space 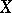over a homogeneous projective rational variety 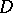, which is universal in the class of all such fibrations. Universality in this case means that the projection 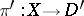of any fibration in this class is representable as 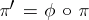, where 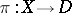is the projection of the Tits bundle and 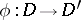is some holomorphic fibering.

An explicit construction of the Tits bundle is carried out as follows. Let 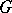be a connected complex Lie group acting holomorphically and transitively on 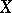, and let 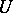be the isotropy subgroup of some point in 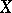. The normalizer 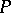of the connected component of the identity of 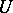is a parabolic subgroup of 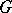, i.e. 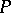contains a maximal connected solvable subgroup (cf. [1], [2]). The base space 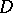of the Tits bundle is defined to be the quotient space 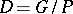, and the projection 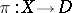is induced by the inclusion of the subgroup 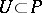. This construction is due to J. Tits [1], who also proved universality for this bundle.

The fibre of the Tits bundle is complex-parallelizable. If the space 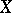is simply-connected, then this fibre is a complex torus. If 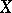admits a transitive group 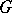equal to its own commutator subgroup, then the Tits bundle coincides with the meromorphic reduction bundle (cf. [3]). This means that all meromorphic functions on 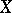are constant on the fibres of the Tits bundle. In the case where the complex compact homogeneous space 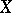is Kähler, the fibre of the Tits bundle is a complex torus (moreover, it is the Albanese variety of 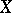), and the bundle itself is analytically trivial [2]. Thus, a compact Kähler homogeneous space is the product of a projective rational homogeneous variety and a complex torus.

References

[1]	J. Tits, "Espaces homogènes complexes compacts" Comment. Math. Helv. , 37 (1962) pp. 111–120
[2]	A. Borel, R. Remmert, "Ueber kompakte homogene Kählerische Mannigfaltigkeiten" Math. Ann. , 145 (1962) pp. 429–439
[3]	H. Grauert, R. Remmert, "Über kompakte homogene komplexe Mannigfaltigkeiten" Arch. Math. , 13 (1962) pp. 498–507