Tie

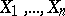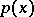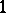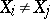A group of observations in a sample that have the same value. Let be independent random variables subject to the same absolutely-continuous probability law with probability density . Then with probability , none of the observations will be equal, that is, if 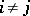, and so every member 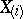of the order statistics (cf. Order statistic)

(*)

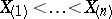constructed from the sample 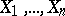will be strictly greater than its predecessor .

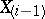However, in practice, because of rounding-off errors in the calculation of 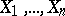, several groups of observations can arise, in each of which the observations are all equal. Every such group of coincident observations is called a tie. Thus, instead of (*), the experimenter may observe the order statistics

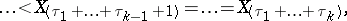where all 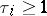and 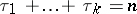. Thus, when ties occur, that is, when some 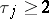, difficulties arise in defining the rank vector, which plays a basic role in the construction of rank statistics (cf. Rank statistic). As yet (1992) there are no precise recommendations for defining the ranks of coincident observations. There are two common approaches to the solution of this problem. The first consists of randomization. According to this approach, the ranks of the elements

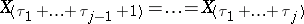making up the the 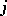-th group are taken to be some permutation of the numbers

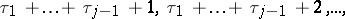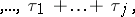each having probability 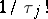. The merit of this approach consists of its simplicity, but for certain alternatives with respect to the distribution of the 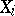, the actual randomization chosen has an effect on the results of the statistical analysis.

In the second approach, all tied observations

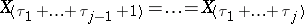making up the 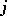-th group are assigned the same, so-called midrank

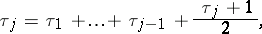equal to the arithmetic mean of the numbers

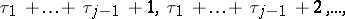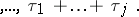It is natural that such a procedure also affects the properties of rank statistics, and this must be taken into account in practice. For example, the second approach is recommended in the construction of the statistics 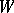of the Wilcoxon test when there are ties. Then the expectation 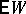of 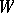remains the same as in the case when there are no ties, but its variance 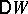decreases to

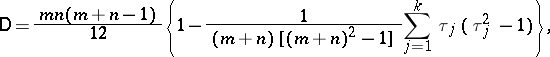and this must be taken into account when normalizing .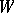

References

[1]	J. Hájek, "Theory of rank tests" , Academia (1967)
[2]	L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova)