Three-series theorem

Kolmogorov three-series theorem, three-series criterion

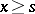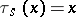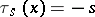For each , let be the truncation function for , for , for .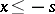

Let be independent random variables with distributions 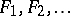. Consider the sums 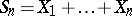, with distributions 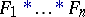. In order that these convolutions tend to a proper limit distribution 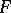as 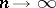, it is necessary and sufficient that for all ,

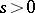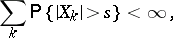(a1)

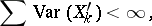(a2)

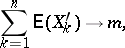(a3)

where .

This can be reformulated as the Kolmogorov three-series theorem: The series 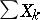converges with probability 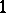if (a1)–(a3) hold, and it converges with probability zero otherwise.

References

[a1]	M. Loève, "Probability theory", Princeton Univ. Press (1963) pp. Sect. 16.3
[a2]	W. Feller, "An introduction to probability theory and its applications", 2, Wiley (1971) pp. Sect. IX.9