Tangent indicatrix
tantrix
The tangent indicatrix 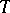 of a regular curve
of a regular curve  is the curve of oriented unit vectors tangent to
is the curve of oriented unit vectors tangent to 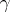 .
.
More precisely, if  is a differentiable curve whose velocity vector
is a differentiable curve whose velocity vector  never vanishes, then
never vanishes, then
 |
The tangent indicatrix 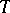 of any regular curve in
of any regular curve in 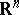 thus traces out a curve on the unit sphere
thus traces out a curve on the unit sphere 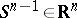 which, as a point set, is independent of the parametrization of
which, as a point set, is independent of the parametrization of 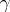 . A direct computation shows that the "speeds" of
. A direct computation shows that the "speeds" of 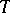 and
and 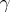 relate via the curvature function
relate via the curvature function 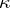 of
of 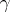 (cf. also Curvature):
(cf. also Curvature):
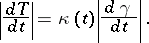 |
It follows immediately that the length of the tangent indicatrix on  gives the total curvature (the integral of
gives the total curvature (the integral of 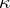 with respect to arc-length; cf. also Complete curvature) of the original curve
with respect to arc-length; cf. also Complete curvature) of the original curve 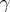 . Because of this, the tangent indicatrix has proven useful, among other things, in studying total curvature of closed space curves (see [a1], p. 29 ff).
. Because of this, the tangent indicatrix has proven useful, among other things, in studying total curvature of closed space curves (see [a1], p. 29 ff).
References
| [a1] | S.S. Chern, "Studies in global analysis and geometry" , Studies in Mathematics , 4 , Math. Assoc. America (1967) |
| [a2] | B. Solomon, "Tantrices of spherical curves" Amer. Math. Monthly , 103 : 1 (1996) pp. 30–39 |
| [a3] | V.I. Arnol'd, "The geometry of spherical curves and the algebra of quaternions" Russian Math. Surveys , 50 : 1 (1995) pp. 1–68 (In Russian) |
Tangent indicatrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tangent_indicatrix&oldid=48947