T 1-space

attainable space

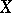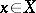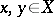A topological space in which the closure of any one-point set coincides with itself. This is equivalent to the requirement that the intersection of all neighbourhoods of a point is identical with or that, for any two different points , there exist neighbourhoods 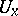and 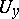of them such that 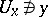and 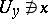, i.e. that the separation axiom 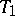holds.

Attainability, i.e. the property that 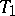holds, is a hereditary property: Any subspace of a 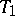-space is a 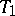-space, and a topology majorizing the topology of a 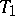-space is a 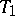-topology. Any 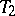-space (cf. Hausdorff space) is 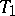-space, but the converse is not true: There exist 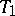-spaces which are not 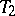-spaces. These include, for example, an infinite set 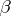with the topology in which the sets with finite complements are considered to be open.

Comments

A very important class of spaces that are 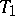but, as a rule, not 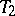are the spectra 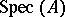of rings 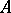with the Zariski topology, cf. Affine scheme.

References

[a1]	R. Engelking, "General topology" , Heldermann (1989)