Syracuse problem

-problem, Collatz problem, Hasse algorithm, Hasse–Collatz problem, Kakutani problem, Ulam problem

This problem concerns the iteration of the Collatz mapping that sends a positive integer to ( even) or to ( odd). The -conjecture (also called the Collatz conjecture) asserts that for any starting value 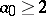there is some iterate .

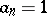Some examples are:

a) ;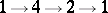

b) ;

c) .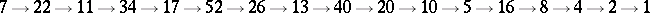

If 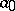is allowed to be a negative integer, the conjecture is not true, as is shown by the example . In other words: the Collatz conjecture with 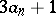replaced by 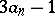does not hold.

This conjecture is generally attributed to L. Collatz, who studied similar problems in the 1930s. It has been numerically verified for all 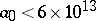[a5]. The conjecture is unsolved (1996) and apparently extremely difficult despite its simple appearance. General references and surveys on the problem are [a3], [a4], [a6].

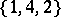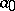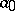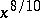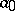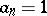There is no periodic orbit of the Collatz mapping of period less than , except the orbit . The set of positive integers that have some iterate less than has density one. At least of all positive integers less than have some iterate , [a1].

J.H. Conway [a2] showed that a certain generalization of the 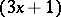-problem is non-computable. He defined a particular mapping 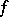from the positive integers into the positive integers of the form 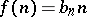, in which is periodic (modulo some 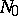) for a fixed modulus 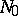, which has the property that the set

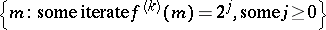is recursively enumerable but not recursive.

References

[a1]	D. Applegate, J.C. Lagarias, "Density bounds for the 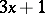problem II. Krasikov inequalities" Math. Comp. , 64 (1995) pp. 427–438
[a2]	J.H. Conway, "Unpredictable Iterations" , Proc. 1972 Number Theory Conf. Univ. Colorado, Boulder (1972) pp. 49–52
[a3]	R.K. Guy, "Unsolved problems in number theory" , Springer (1994) pp. Problem E16 (Edition: Second)
[a4]	J.C. Lagarias, "The 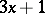problem and its generalizations" Amer. Math. Monthly , 92 (1985) pp. 3–23
[a5]	G. Leavens, M. Vermeulen, "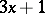 search programs" Computers & Mathematics, with Applications , 24 : 11 (1992) pp. 79–99
[a6]	H.A. Müller, "Das "3n+1" Problem" Mitteil. Math. Ges. Hamburg , 12 (1991) pp. 231–251