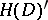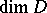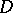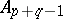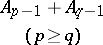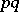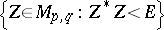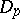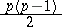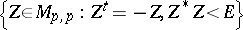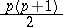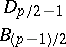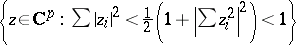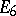Symmetric domain

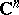A complex manifold isomorphic to a bounded domain in and such that, for every point 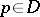, there is an involutory holomorphic transformation 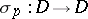with 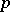as unique fixed point. A symmetric domain is a Hermitian symmetric space of negative curvature with respect to the Bergman metric (cf. Bergman kernel function). Its automorphism group is contained, as a complex manifold, in the group of motions and has the same connected component 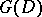, which is a non-compact real semi-simple Lie group without centre. 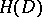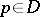The stationary subgroup of in 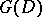is a connected compact Lie group with one-dimensional centre. As a real manifold, a symmetric domain is diffeomorphic to .

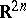Every symmetric domain is uniquely decomposable as a direct product of irreducible symmetric domains, and these are listed in the following table (where 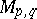denotes the space of complex 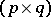-matrices).'

<tbody> </tbody> Cartan type Type of Type of Model of I II III IV V 16 VI 27

A symmetric domain of type III can be represented as the Siegel upper half-plane:

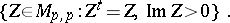Its points parametrize principally polarized Abelian varieties. The other symmetric domains can also be represented as Siegel domains (cf. Siegel domain) of the first or second kind (see [2]).

References

[1]	C.L. Siegel, "Automorphe Funktionen in mehrerer Variablen" , Math. Inst. Göttingen (1955)
[2]	I.I. [I.I. Pyatetskii-Shapiro] Piatetski-Shapiro, "Automorphic functions and the geometry of classical domains" , Gordon & Breach (1969) (Translated from Russian)
[3]	E. Cartan, "Domains bornés homogènes de l'espace de variables complexes" Abh. Math. Sem. Univ. Hamburg , 1 (1935) pp. 116–162
[4]	D. Drucker, "Exceptional Lie algebras and the structure of hermitian symmetric spaces" , Amer. Math. Soc. (1978)

Comments

The stationary subgroup 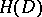has one-dimensional centre if and only if the symmetric domain is irreducible.

References

[a1]	S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) pp. Chapt. X