Symmetric difference of order n
From Encyclopedia of Mathematics
at a point 
of a function 
of a real variable
The expression
 |
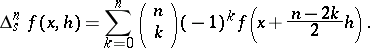The following expression is often also referred to as a symmetric difference:
 |
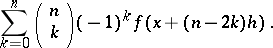It is obtained from the above by substituting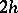 
for 
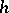. If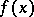 
has an 
-th order derivative 
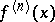at 
, then
 |
Comments
References
| [a1] | H. Meschkowski, "Differenzengleichungen" , Vandenhoeck & Ruprecht (1959) |
| [a2] | L.N. Milne-Thomson, "The calculus of finite differences" , Chelsea, reprint (1981) |
| [a3] | N.E. Nörlund, "Volesungen über Differenzenrechnung" , Chelsea, reprint (1954) |
How to Cite This Entry:
Symmetric difference of order n. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_difference_of_order_n&oldid=48924
Symmetric difference of order n. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_difference_of_order_n&oldid=48924
This article was adapted from an original article by T.P. Lukashenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article