Symmetric derived number
From Encyclopedia of Mathematics
at a point 
A generalization of the ordinary notion of a derived number (cf. Dini derivative) to the case of a set function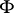 
on an 
-dimensional Euclidean space. The symmetric derived numbers of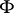 
at 
are defined as the limits
 |
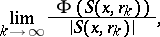where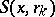 
is some sequence of closed balls with centres at 
and radii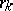 
such that 
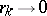as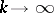 
.
The 
-th symmetric derived numbers at 
of a function 
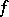of a real variable are defined as the limits
 |
 |
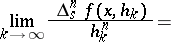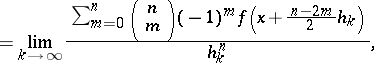where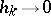 
as 
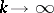and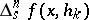 
is the symmetric difference of order 
of 
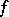at 
.
References
| [1] | S. Saks, "Theory of the integral" , Hafner (1937) (Translated from French) |
Comments
References
| [a1] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1974) pp. 24 |
How to Cite This Entry:
Symmetric derived number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_derived_number&oldid=48923
Symmetric derived number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_derived_number&oldid=48923
This article was adapted from an original article by T.P. Lukashenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article