Swerve of a curve
From Encyclopedia of Mathematics
self-rotation of a curve
The part of the variation of the rotation of a curve on an irregular surface not caused by the concentration of the integral curvature of the surface on the set of points of the curve. For a simple arc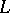 
, the swerve is equal to 
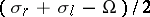, where 
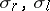are the variations under right and left traversal of 
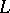, while 
is the variation of the curvature of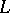 
as a set. Curves with swerve zero are called quasi-geodesic curves (cf. Quasi-geodesic line).
References
| [1] | A.D. Aleksandrov, V.V. Strel'tsov, "Isoperimetric problems and estimates of the length of a curve on a surface" Proc. Steklov Inst. Math. , 76 (1965) pp. 81–99 Trudy Mat. Inst. Steklov. , 76 (1965) pp. 67–80 |
Comments
References
| [a1] | H. Busemann, "Convex surfaces" , Interscience (1958) pp. Chapt. III, Sect. 15 |
How to Cite This Entry:
Swerve of a curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Swerve_of_a_curve&oldid=48918
Swerve of a curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Swerve_of_a_curve&oldid=48918
This article was adapted from an original article by Yu.D. Burago (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article