Supergraph
From Encyclopedia of Mathematics
of a function
Let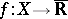 
be a function defined on some set 
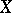with values in the extended real line 
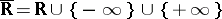. Then the supergraph of 
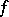is the subset of the Cartesian product 
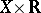consisting of all points 
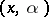lying "above" the graph of 
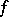. The supergraph is sometimes called the epigraph and is denoted by 
:
 |
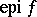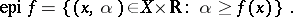The projection of the supergraph onto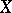 
is known as the effective domain of 
, denoted by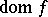 
:
 |
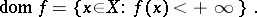The function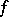 
is said to be proper if
 |
A function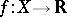 
defined on a real vector space 
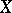is convex if and only if 
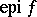is a convex subset of 
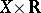. A function 
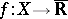defined on a topological space 
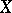is upper semi-continuous if and only if 
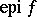is a closed set.
Comments
References
| [a1] | R.T. Rockafellar, "Convex analysis" , Princeton Univ. Press (1970) pp. 23; 307 |
How to Cite This Entry:
Supergraph. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Supergraph&oldid=48912
Supergraph. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Supergraph&oldid=48912
This article was adapted from an original article by V.M. Tikhomirov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article