Summability, strong
of a complex sequence  of numbers or functions (or of a series
of numbers or functions (or of a series 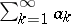 with partial sums
with partial sums 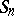 ) to a number
) to a number 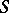
Summability by a method 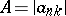 (cf. Summation methods) such that for a certain
(cf. Summation methods) such that for a certain 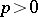 :
:
1) the sequence
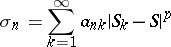 |
converges for every 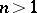 , and for almost all
, and for almost all  in the case of a sequence of functions;
in the case of a sequence of functions;
2) 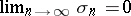 . By retaining 2) and replacing 1) by:
. By retaining 2) and replacing 1) by:
1') for every monotone increasing sequence of indices 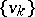 , the sequence
, the sequence
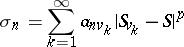 |
converges for every 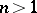 , and for almost all
, and for almost all  in the case of a sequence of functions, one arrives at the concept of very strong summability.
in the case of a sequence of functions, one arrives at the concept of very strong summability.
The concept of strong summability was introduced in connection with the  -summability of Fourier series (cf. Summation of Fourier series). The importance of this concept is well illustrated in the example of strong
-summability of Fourier series (cf. Summation of Fourier series). The importance of this concept is well illustrated in the example of strong 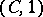 -summability. Strong
-summability. Strong  -summability signifies that the partial sums
-summability signifies that the partial sums  that spoil the convergence of the sequence
that spoil the convergence of the sequence 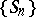 are sufficiently scarcely positioned, i.e. have zero density. Unlike strong summability, very strong summability means that the convergence of the sequence
are sufficiently scarcely positioned, i.e. have zero density. Unlike strong summability, very strong summability means that the convergence of the sequence  is spoiled by very thin sequences
is spoiled by very thin sequences  .
.
References
| [1] | G.H. Hardy, J.E. Littlewood, "Sur la série de Fourier d'une fonction à carré sommable" C.R. Acad. Sci. Paris , 156 (1913) pp. 1307–1309 |
| [2] | G. Aleksich, "Convergence problems of orthogonal series" , Pergamon (1961) (Translated from Russian) |
| [3] | A. Zygmund, "Trigonometric series" , 2 , Cambridge Univ. Press (1988) |
| [4] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [5] | Gen-Ichirô Sunouchi, "Strong summability of Walsh–Fourier series" Tôhoku Math. J. , 16 (1964) pp. 228–237 |
| [6] | Gen-Ichirô Sunouchi, Acta Sci. Math. , 27 : 1–2 (1966) pp. 71–76 |
| [7] | V.A. Bolgov, E.V. Efimov, "On the rate of summability of orthogonal series" Math. USSR Izv. , 5 : 6 (1071) pp. 1399–1417 Izv. Akad. Nauk SSSR Ser. Mat. , 35 : 6 (1971) pp. 1389–1408 |
| [8] | Z. Zatewasser, Studia Math. , 6 (1936) pp. 82–88 |
| [9] | L. Leindler, "Ueber die sehr starke Riesz-Summierbarkeit der Orthogonalreihen und Konvergenz lückenhafter Orthogonalreihen" Acta Math. Acad. Sci. Hung. , 13 : 3–4 (1962) pp. 401–414 |
Summability, strong. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Summability,_strong&oldid=48905