Subparabolic function

subcaloric function

The analogue of a subharmonic function for the heat equation

(*)

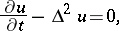where , and is the Laplace operator. For example, a function , , , of class will be a subparabolic function in the rectangle

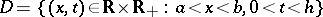if

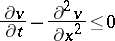everywhere in . In a more general case, let the poin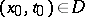t , let 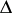be a sufficiently small equilateral triangle with base parallel to the axis 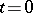and let 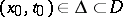. A function 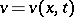that is continuous in the closed domain 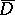is said to be subparabolic in if its value at any point 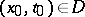is not greater than the value at this point of that solution of (*) in any sufficiently small triangle 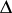, , 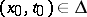that has the same values on the sides of 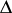as .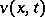

Many properties of subharmonic functions, including the maximum principle, are also valid for subparabolic functions.

References

[1]	V.I. Smirnov, "A course of higher mathematics" , 2 , Addison-Wesley (1964) (Translated from Russian)
[2]	I.G. Petrovskii, "Partial differential equations" , Saunders (1967) (Translated from Russian)
[3]	I.G. Petrovskii, "Zur ersten Randwertaufgabe der Wärmeleitungsgleichung" Compos. Math. , 1 (1935) pp. 383–419

Comments

See [a1] for an account of subparabolic functions from a potential-theoretic point of view.

References

[a1]	J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1983)
[a2]	A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964)