Strong extremum
A minimal or maximal value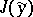 
taken by a functional 
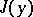at a curve 
, 
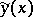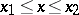, for which one of the inequalities
 |
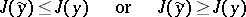holds for all comparison curves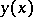 
in an 
-neighbourhood of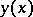 
. The curves 
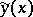and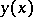 
must satisfy given boundary conditions.
Since maximization of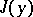 
is equivalent to minimization of 
, instead of a strong maximum one often discusses only a strong minimum. The term "strong" emphasizes that only the condition of being 
-near to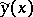 
is imposed on the comparison curves 
:
 |
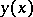on the whole interval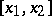 
, whereas the derivatives of the curves 
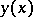and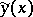 
may differ as "strongly" as desired.
However, the very definition of a strong extremum is of a relative rather than absolute nature, since it gives an extremum not on the whole class of admissible comparison curves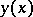 
for which 
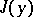makes sense, but only relative to the subset of all admissible comparison curves belonging to the 
-neighbourhood of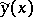 
. However, for brevity, the term "relative" is often omitted and one speaks of a strong extremum, meaning a strong relative extremum (see also Strong relative minimum).
References
| [1] | M.A. Lavrent'ev, L.A. Lyusternik, "A course in variational calculus" , Moscow-Leningrad (1950) (In Russian) |
| [2] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian) |
Comments
References
| [a1] | L. Cesari, "Optimization - Theory and applications" , Springer (1983) |
Strong extremum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strong_extremum&oldid=48875