Strip method (integral equations)

A method for the approximate solution of one-dimensional Fredholm integral equations of the second kind (cf. also Fredholm equation; Fredholm equation, numerical methods), based on replacing the kernel in a special way by a degenerate kernel, evaluating the resolvent of the degenerate equation and then improving the approximate solution through the use of a rapidly-convergent iterative algorithm.

Let the original integral equation be written as

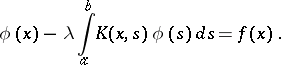(1)

To construct the degenerate kernel, divide the square

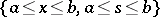into 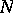strips

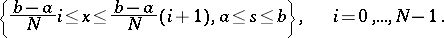In each strip, say the 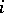-th, the function 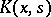is approximated in the mean square, or uniformly, by functions

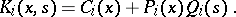In the simplest case,

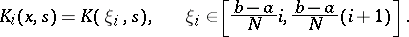The function 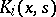is now used to construct a degenerate kernel:

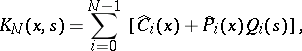(2)

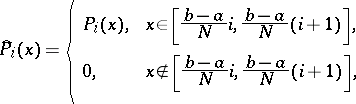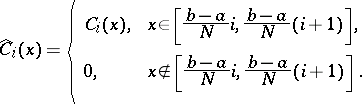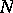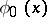The solution of the equation with the degenerate kernel (2) approximates the solution of equation (1), generally, the better the larger the number of strips and the better the approximation of in each strip is. The approximate solution can be further improved by using the iterative algorithm

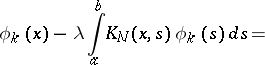(3)

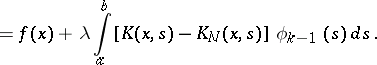The iterations (3) converge in the mean square, or uniformly, to the solution of equation (1), provided the kernels 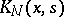approach .

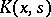References

[1]	G.N. Polozhii, P.I. Chalenko, "The strip method for solving integral equations" Dop. Akad. Nauk UkrSSR : 4 (1962) pp. 427–431 (In Ukrainian) ((English abstract.))

Comments

Excellent surveys on the numerical solution of Fredholm equations of the second kind can be found in [a1] and [a2]; the strip method is not mentioned there, although other degenerate kernel methods are discussed, cf. also Degenerate kernels, method of.

References

[a1]	K.E. Atkinson, "A survey of numerical methods for the solution of Fredholm integral equations of the second kind" , SIAM (1976)
[a2]	C.T.H. Baker, "The numerical treatment of integral equations" , Clarendon Press (1977) pp. Chapt. 4