Strip method (analytic functions)

A method in the theory of functions of a complex variable that is based on inequalities relating the lengths of curves of a certain special family and the area of the domain occupied by this family. The method is based on Grötzsch' lemmas . One of them is formulated as follows.

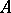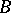Consider a rectangle with sides of lengths and which contains a finite number of non-overlapping simply-connected domains 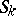, , 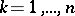each one having a Jordan boundary that meets the sides of length 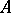in segments which do not degenerate into points (the regions 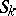form strips running from one side of length 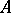to the other). If 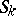is conformally mapped into a rectangle with sides of lengths 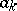and 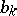such that the above segments become the sides of length 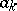, then

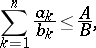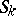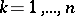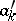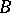with equality attained only if the , , are rectangles with sides of length and with .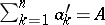

Another lemma is the Grötzsch principle. The Grötzsch lemmas are true also for an infinite set of subdomains.

The strip method as a method in the theory of univalent conformal and quasi-conformal mapping was first used by H. Grötzsch , who used the method in a systematic study and solved numerous extremal problems for univalent functions defined in finitely-connected and infinitely-connected domains (see [3]; for other applications, see [2]).

The method also forms the basis of the method of the extremal metric (cf. Extremal metric, method of the).

References

[1a]	H. Grötzsch, "Über einige Extremalprobleme der konformen Abbildung I" Ber. Verh. Sächsisch. Akad. Wiss. Leipzig. Math.-Phys. Kl. , 80 : 6 (1928) pp. 367–376
[1b]	H. Grötzsch, "Über die Verzerrung bei schlichten nichtkonformen Abbildungen und über eine damit zusammenhängende Erweiterung des Picardschen Satzes" Ber. Verh. Sächsisch. Akad. Wiss. Leipzig. Math.-Phys. Kl. , 80 : 7 (1929) pp. 503–507
[1c]	H. Grötzsch, "Über die Verzerrung bei schlichter konformer Abbildung mehrfach zusammenhängender schlichter Bereiche" Ber. Verh. Sächsisch. Akad. Wiss. Leipzig. Math.-Phys. Kl. , 81 : 1 (1929) pp. 38–48
[1d]	H. Grötzsch, "Über konforme Abbildung unendlichvielfach zusammenhängender schlichter Bereiche mit endlichvielen Häufungsrandkomponenten" Ber. Verh. Sächsisch. Akad. Wiss. Leipzig. Math.-Phys. Kl. , 81 : 2 (1929) pp. 51–87
[2]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)
[3]	J.A. Jenkins, "Univalent functions and conformal mapping" , Springer (1958)