Strip (generalized)
surface strip (in the narrow sense)
A one-parameter family of planes tangent to a surface. In the general sense, a strip is the union of a curve 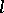 and a vector
and a vector 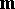 orthogonal to the tangent vector of the curve at each of its points. Suppose that
orthogonal to the tangent vector of the curve at each of its points. Suppose that 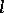 is given in the space
is given in the space 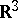 by an equation
by an equation 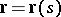 , where
, where  is the natural parameter of the curve and
is the natural parameter of the curve and 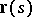 is the position vector of the points of the curve. Along
is the position vector of the points of the curve. Along 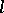 one has a vector-function
one has a vector-function 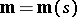 , where
, where  is a unit vector orthogonal to the tangent vector
is a unit vector orthogonal to the tangent vector  at the corresponding points of the curve. One then says that a surface strip
at the corresponding points of the curve. One then says that a surface strip 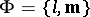 with normal
with normal  is defined along
is defined along 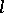 . The vector
. The vector  is called the geodesic normal vector of
is called the geodesic normal vector of 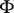 ; together with
; together with 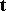 and
and 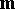 , the vector
, the vector  forms the Frénet frame for the strip. Given the moving Frénet frame for a strip, one has the Frénet derivation formulas:
forms the Frénet frame for the strip. Given the moving Frénet frame for a strip, one has the Frénet derivation formulas:
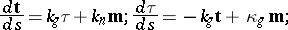 |
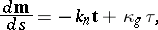 |
where 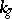 denotes the geodesic curvature of the strip,
denotes the geodesic curvature of the strip, 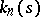 denotes its normal curvature and
denotes its normal curvature and 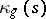 denotes its geodesic torsion, which are scalar functions of
denotes its geodesic torsion, which are scalar functions of  .
.
If the vector 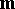 is collinear with the principal normal at each point of
is collinear with the principal normal at each point of 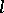 , then
, then 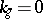 and the strip is then called a geodesic strip. If
and the strip is then called a geodesic strip. If 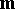 is collinear with the binormal of the curve at each point, one has
is collinear with the binormal of the curve at each point, one has  and the strip is called an asymptotic strip.
and the strip is called an asymptotic strip.
References
| [1] | W. Blaschke, "Einführung in die Differentialgeometrie" , Springer (1950) |
Strip (generalized). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strip_(generalized)&oldid=48872