Stochastic process, differentiable

A stochastic process 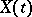such that the limit

exists; it is called the derivative of the stochastic process 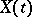. One distinguishes between differentiation with probability 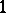and mean-square differentiation, according to how this limit is interpreted. The condition of mean-square differentiability can be naturally expressed in terms of the correlation function

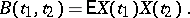Namely, 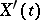exists if and only if the limit

exists. A stochastic process having a mean-square derivative is absolutely continuous. More precisely, for every 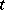and with probability 1,

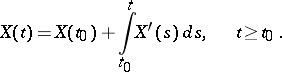A sufficient condition for the existence of a process equivalent to a given one with continuously differentiable trajectories is that its mean square-derivative 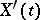is continuous and has 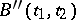as its correlation function. For Gaussian processes this condition is also necessary.

References

[1]	I.I. Gikhman, A.V. Skorokhod, "Introduction to the theory of stochastic processes" , Saunders (1967) (Translated from Russian)

Comments

For additional references see Stochastic process.