Stirling interpolation formula
From Encyclopedia of Mathematics
The half-sum of the Gauss interpolation formula for forward interpolation with respect to the nodes 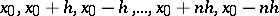 at the point
at the point 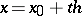 :
:
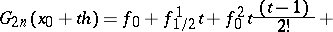 |
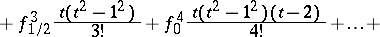 |
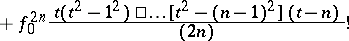 |
and Gauss' formula of the same order for backward interpolation with respect to the nodes 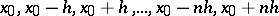 :
:
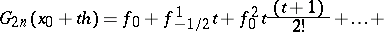 |
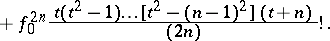 |
Using the notation
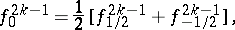 |
Stirling's interpolation formula takes the form:
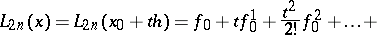 |
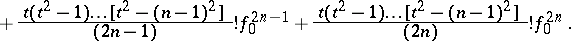 |
For small 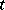 , Stirling's interpolation formula is more exact than other interpolation formulas.
, Stirling's interpolation formula is more exact than other interpolation formulas.
References
| [1] | I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian) |
Comments
The central differences 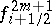 and
and 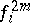 (
(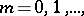
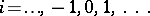 ) are defined recursively from the (tabulated values)
) are defined recursively from the (tabulated values) 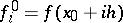 by the formulas
by the formulas
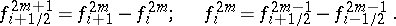 |
References
| [a1] | F.B. Hildebrand, "Introduction to numerical analysis" , Dover, reprint (1987) pp. 139 |
How to Cite This Entry:
Stirling interpolation formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stirling_interpolation_formula&oldid=48843
Stirling interpolation formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stirling_interpolation_formula&oldid=48843
This article was adapted from an original article by M.K. Samarin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article