Steklov function

for an integrable function 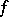on a bounded segment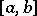

The function

(*)

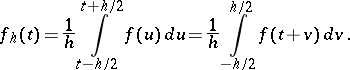Functions of the form (*), as well as the iteratively defined functions

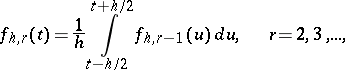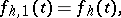were first introduced in 1907 by V.A. Steklov (see [1]) in solving the problem of expanding a given function into a series of eigenfunctions. The Steklov function 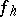has derivative

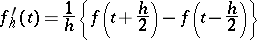almost everywhere. If 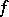is uniformly continuous on the whole real axis, then

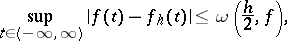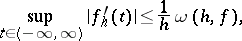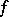where is the modulus of continuity of . Similar inequalities hold in the metric of 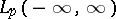, provided .

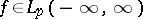References

[1]	V.A. Steklov, "On the asymptotic representation of certain functions defined by a linear differential equation of the second order, and their application to the problem of expanding an arbitrary function into a series of these functions" , Khar'kov (1957) (In Russian)
[2]	N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian)

Comments

Steklov's fundamental paper was first published in French (1907) in the "Communications of the Mathematical Society of Kharkov" ; [1] is the Russian translation, together with additional comments by N.S. Landkof.

References

[a1]	E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982)
[a2]	M.W. Müller, "Approximationstheorie" , Akad. Verlagsgesellschaft (1978)