Star body

with respect to a point 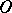, star-like body

An open set 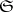in -dimensional Euclidean space 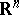which has the ray property (relative to 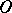): If 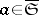, where 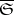is the closure of 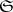, then the entire segment 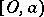(where 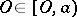, 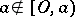) lies in 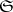. A star body 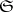with centre 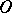may be characterized as follows: 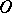is an interior point of 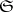; every ray emanating from 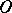lies either entirely in 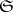or contains a point such that the ray segment 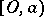lies in 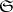, but the ray segment 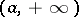lies outside 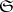. This definition is equivalent to the first one, up to points on the boundary of 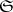. A star body is a particular case of a star set with respect to 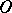, a set with the generalized ray property relative to 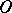: If , then the entire segment 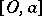lies in 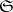. A particular case of a star body is a convex body.

With every star body 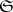with respect to the origin 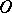one can associate, in one-to-one fashion, a ray function 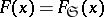such that 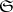is the set of points with .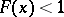

The correspondence is defined by the formula

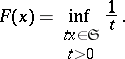With this notation a star body 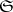is bounded if and only if is a positive ray function; it is convex if and only if 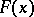is a convex ray function.

References

[1]	J.W.S. Cassels, "An introduction to the geometry of numbers" , Springer (1972)

Comments

Star bodies play an important role in the geometry of numbers, e.g. the Minkowski–Hlawka theorem.

A set in 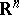is centrally symmetric if implies .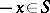

The Minkowski–Hlawka theorem says that 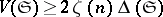for a centrally-symmetric star body 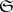. Here, 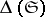is the critical determinant of 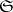(cf. Geometry of numbers), 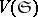is the volume of 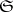and . This is an inequality in the opposite direction of the Minkowski convex body theorem (cf. Minkowski theorem).

References

[a1]	P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint)
[a2]	P. Erdös, P.M. Gruber, J. Hammer, "Lattice points" , Longman (1989)