Stability for a part of the variables
Lyapunov stability of the solution 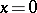 relative not to all but only to certain variables
relative not to all but only to certain variables  ,
,  , of a system of ordinary differential equations
, of a system of ordinary differential equations
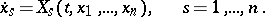 | (1) |
Here 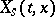 are given real-valued continuous functions, satisfying in the domain
are given real-valued continuous functions, satisfying in the domain
 | (2) |
the conditions for the existence and uniqueness of the solution 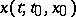 ; moreover,
; moreover,
 |
and any solution is defined for all  for which
for which 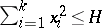 .
.
Put 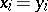 for
for 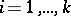 ;
; 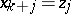 for
for 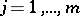 ,
, 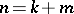 and
and 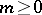 ; let
; let
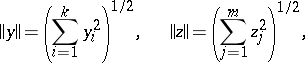 |
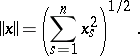 |
The solution 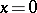 of the system (1) is called: a) stable relative to
of the system (1) is called: a) stable relative to  or
or 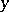 -stable if
-stable if
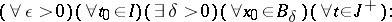 |
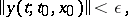 |
i.e. for any given numbers 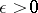 (
(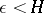 ) and
) and 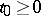 one can find a number
one can find a number 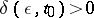 such that for every perturbation
such that for every perturbation 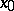 satisfying the condition
satisfying the condition 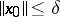 and for every
and for every 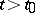 the solution
the solution 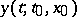 satisfies the condition
satisfies the condition 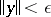 ;
;
b) 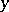 -unstable in the opposite case, i.e. if
-unstable in the opposite case, i.e. if
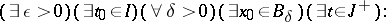 |
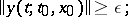 |
c) 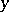 -stable uniformly in
-stable uniformly in 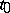 if in definition a) for every
if in definition a) for every 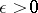 the number
the number 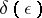 may be chosen independently of
may be chosen independently of 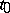 ;
;
d) asymptotically  -stable if it is
-stable if it is 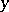 -stable and if for every
-stable and if for every 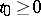 there exists a
there exists a 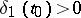 such that
such that
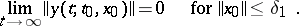 |
Here 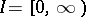 ,
, 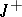 is the maximal right interval on which
is the maximal right interval on which 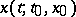 is defined,
is defined, 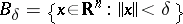 ; in case d), besides the conditions stated above it is assumed that all solutions of the system (1) exist on
; in case d), besides the conditions stated above it is assumed that all solutions of the system (1) exist on 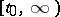 .
.
The statement of the problem of stability for a part of the variables was given by A.M. Lyapunov [1] as a generalization of the stability problem with respect to all variables 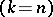 . For a solution of this problem it is particularly effective to apply the method of Lyapunov functions, suitably modified (cf. [2], and Lyapunov function) for the problem of
. For a solution of this problem it is particularly effective to apply the method of Lyapunov functions, suitably modified (cf. [2], and Lyapunov function) for the problem of 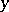 -stability. At the basis of this method there are a number of theorems generalizing the classical theorem of Lyapunov.
-stability. At the basis of this method there are a number of theorems generalizing the classical theorem of Lyapunov.
Consider a real-valued function 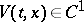 ,
, 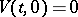 , and at the same time its total derivative with respect to time, using (1):
, and at the same time its total derivative with respect to time, using (1):
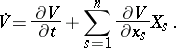 |
A function 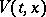 of constant sign is called
of constant sign is called 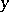 -sign-definite if there exists a positive-definite function
-sign-definite if there exists a positive-definite function 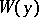 such that in the region (2),
such that in the region (2),
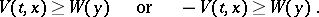 |
A bounded function 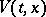 is said to admit an infinitesimal upper bound for
is said to admit an infinitesimal upper bound for 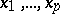 if for every
if for every 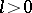 there exists a
there exists a 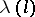 such that
such that
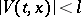 |
for 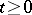 ,
, 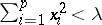 ,
,  .
.
Theorem 1.
If the system (1) is such that there exists a 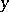 -positive-definite function
-positive-definite function 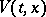 with derivative
with derivative 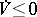 , then the solution
, then the solution 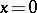 is
is  -stable.
-stable.
Theorem 2.
If the conditions of theorem 1 are fulfilled and if, moreover,  admits an infinitesimal upper bound for
admits an infinitesimal upper bound for  , then the solution
, then the solution 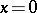 of the system (1) is
of the system (1) is 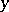 -stable uniformly in
-stable uniformly in 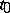 .
.
Theorem 3.
If the conditions of theorem 1 are fulfilled and if, moreover, 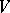 admits an infinitesimal upper bound for
admits an infinitesimal upper bound for 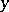 , then for any
, then for any 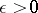 one can find a
one can find a  such that
such that 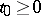 ,
, 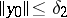 ,
, 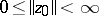 implies the inequality
implies the inequality
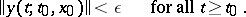 |
Theorem 4.
If the system (1) is such that there exists a 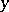 -positive-definite function
-positive-definite function 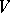 admitting an infinitesimal upper bound for
admitting an infinitesimal upper bound for 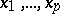 (
(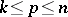 ) and with negative-definite derivative
) and with negative-definite derivative 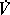 for
for 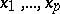 , then the solution
, then the solution 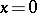 of the system (1) is asymptotically
of the system (1) is asymptotically 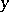 -stable.
-stable.
For the study of  -instability, Chetaev's instability theorem (cf. Chetaev function) has been successfully applied, as well as certain other theorems. Conditions for the converse of a number of theorems on
-instability, Chetaev's instability theorem (cf. Chetaev function) has been successfully applied, as well as certain other theorems. Conditions for the converse of a number of theorems on 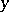 -stability have been established; for example, the converses of theorems 1, 2 as well as of theorem 4 for
-stability have been established; for example, the converses of theorems 1, 2 as well as of theorem 4 for 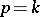 . Methods of differential inequalities and Lyapunov vector functions have been applied to establish theorems on asymptotic
. Methods of differential inequalities and Lyapunov vector functions have been applied to establish theorems on asymptotic 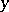 -stability in the large, on first-order approximations, etc. (cf. [3], ).
-stability in the large, on first-order approximations, etc. (cf. [3], ).
References
| [1] | A.M. Lyapunov, Mat. Sb. , 17 : 2 (1893) pp. 253–333 |
| [2] | V.V. Rumyantsev, "On stability of motion for a part of the variables" Vestn. Moskov. Univ. Ser. Mat. Mekh. Astron. Fiz. Khim. : 4 (1957) pp. 9–16 (In Russian) |
| [3] | A.S. Oziraner, V.V. Rumyantsev, "The method of Lyapunov functions in the stability problem for motion with respect to a part of the variables" J. Appl. Math. Mech. , 36 (1972) pp. 341–362 Prikl. Mat. i Mekh. , 36 : 2 (1972) pp. 364–384 |
Comments
Stability for a part of the variables is also called partial stability and occasionally conditional stability, [a1]. However, the latter phrase is also used in a different meaning: Let 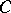 be a class of trajectories,
be a class of trajectories, 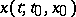 a trajectory in
a trajectory in 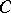 . This trajectory is stable relative to
. This trajectory is stable relative to 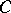 if for a given
if for a given  there exists a
there exists a 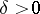 such that for each trajectory
such that for each trajectory 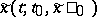 one has that
one has that 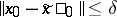 implies
implies 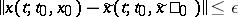 . If
. If 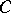 is not the class of all trajectories, such a
is not the class of all trajectories, such a 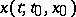 is called conditionally stable, [a2].
is called conditionally stable, [a2].
References
| [a1] | W. Hahn, "Stability of motion" , Springer (1965) pp. §55 |
| [a2] | S. Lefshetz, "Differential equations: geometric theory" , Dover, reprint (1977) pp. 78, 83 |
Stability for a part of the variables. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stability_for_a_part_of_the_variables&oldid=48790