Spinor representation

spin representation

The simplest faithful linear representation (cf. Faithful representation; Linear representation) of the spinor group 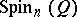, or the linear representation of the corresponding even Clifford algebra 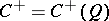(see Spinor group; 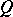is a quadratic form). If the ground field 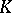is algebraically closed, then the algebra is isomorphic to the complete matrix algebra (where ) or to the algebra (where 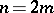). Therefore there is defined a linear representation 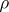of the algebra 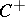on the space of dimension 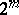over 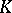; this representation is called a spinor representation. The restriction of 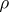to 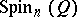is called the spinor representation of 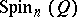. 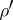For odd , the spinor representation is irreducible, and for even it splits into the direct sum of two non-equivalent irreducible representations and 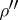, which are called half-spin (or) representations. The elements of the space of the spinor representation are called spinors, and those of the space of the half-spinor representation half-spinors. The spinor representation of the spinor group 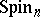is self-dual for any 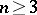, whereas the half-spinor representations 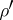and 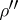of the spinor group 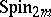are self-dual for even 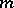and dual to one another for odd . The spinor representation of 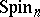is faithful for all 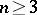, while the half-spinor representations of 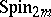are faithful for odd 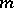, but have a kernel of order two when is even.

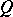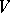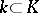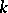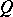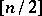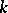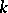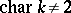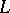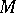For a quadratic form on a space over some subfield , the spinor representation is not always defined over . However, if the Witt index of is maximal, that is, equal to (in particular, if is algebraically closed), then the spinor and half-spinor representations are defined over . In this case these representations can be described in the following way if (see [1]). Let and be 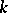-subspaces of the 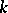-space 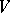that are maximal totally isotropic (with respect to the symmetric bilinear form on 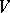associated with 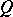) and 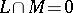let . Let 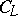be the subalgebra of the Clifford algebra 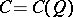generated by the subspace 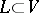, and let 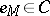be the product of 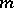vectors forming a -basis of . If is even, 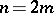, then the spinor representation is realized in the left ideal 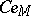and acts there by left translation: 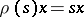(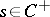, 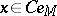). Furthermore, the mapping 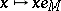defines an isomorphism of vector spaces 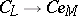that enables one to realize the spinor representation in 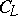, which is naturally isomorphic to the exterior algebra over 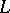. The half-spinor representations 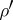and 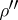are realized in the 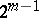-dimensional subspaces 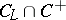and .

If is odd, then 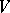can be imbedded in the 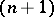-dimensional vector space 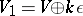over 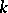. One defines a quadratic form 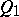on by putting 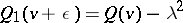for all and 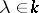. 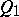is a non-degenerate quadratic form of maximal Witt index defined over 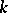on the even-dimensional vector space 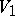. The spinor representation of 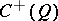(or of 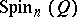) is obtained by restricting any of the half-spinor representations of 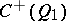(or of 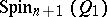) to the subalgebra 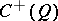(or 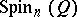, respectively).

The problem of classifying spinors has been solved when and 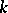is an algebraically closed field of characteristic 0 (see [4], [8], [9]). The problem consists of the following: 1) describe the orbits of in the spinor space by giving a representative of each orbit; 2) calculate the stabilizers in 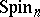of each of these representatives; and 3) describe the algebra of invariants of the linear group .

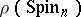The existence of spinor and half-spinor representations of the Lie algebra of 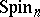was discovered by E. Cartan in 1913, when he classified the finite-dimensional representations of simple Lie algebras [6]. In 1935, R. Brauer and H. Weyl described spinor and half-spinor representations in terms of Clifford algebras [5]. P. Dirac [3] showed how spinors could be used in quantum mechanics to describe the rotation of an electron.

References

[1]	N. Bourbaki, "Algèbre" , Eléments de mathématiques , Hermann (1970) pp. Chapt. II. Algèbre linéaire MR0274237 Zbl 0211.02401
[2]	H. Weyl, "Classical groups, their invariants and representations" , Princeton Univ. Press (1946) (Translated from German) MR0000255 Zbl 1024.20502
[3]	P.A.M. Dirac, "Principles of quantum mechanics" , Clarendon Press (1958) MR2303789 MR0116921 MR0023198 MR1522388 Zbl 0080.22005
[4]	V.L. Popov, "Classification of spinors of dimension fourteen" Trans. Moscow Math. Soc. , 1 (1980) pp. 181–232 Trudy Moskov. Mat. Obshch. , 37 (1978) pp. 173–217 MR0514331 Zbl 0443.20038
[5]	R. Brauer, H. Weyl, "Spinors in -dimensions" Amer. J. Math. , 57 : 2 (1935) pp. 425–449 MR1507084
[6]	E. Cartan, "Les groupes projectifs qui ne laissant invariante aucune multiplicité plane" Bull. Soc. Math. France , 41 (1913) pp. 53–96
[7]	C. Chevalley, "The algebraic theory of spinors" , Columbia Univ. Press (1954) MR0060497 Zbl 0057.25901
[8]	V. Gatti, E. Viniberghi, "Spinors in 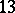-dimensional space" Adv. Math. , 30 : 2 (1978) pp. 137–155
[9]	J.I. Igusa, "A classification of spinors up to dimension twelve" Amer. J. Math. , 92 : 4 (1970) pp. 997–1028 MR0277558 Zbl 0217.36203