spectral cumulant
One of the characteristics of a stationary stochastic process. Let  ,
,  , be a real stationary stochastic process for which
, be a real stationary stochastic process for which  . The semi-invariants (cf. Semi-invariant) of this process,
. The semi-invariants (cf. Semi-invariant) of this process,
are connected with the moments
by the relations
where
and the summation is over all partitions of 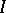 into disjoint subsets
into disjoint subsets  . It is said that
. It is said that  if, for all
if, for all 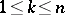 , there is a complex measure of bounded variation
, there is a complex measure of bounded variation 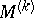 on
on  such that for all
such that for all  ,
,
A measure  , defined on a system of Borel sets, is called a spectral semi-invariant if, for all
, defined on a system of Borel sets, is called a spectral semi-invariant if, for all  ,
,
The measure  exists and has bounded variation if
exists and has bounded variation if 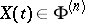 . In the case of a stationary process
. In the case of a stationary process 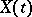 , the semi-invariants
, the semi-invariants  are invariant under translation:
are invariant under translation:
and the spectral measures  and
and  are concentrated on the manifold
are concentrated on the manifold  . If the measure
. If the measure  is absolutely continuous with respect to Lebesgue measure on this manifold, then there is a spectral density
is absolutely continuous with respect to Lebesgue measure on this manifold, then there is a spectral density  of order
of order  , defined by the equations
, defined by the equations
for all  . In the case of discrete time one must replace
. In the case of discrete time one must replace  in all formulas above by the
in all formulas above by the 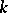 -dimensional cube
-dimensional cube  ,
,  .
.
References
| [1] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) |
| [2] | V.P. Leonov, "Some applications of higher semi-invariants to the theory of stationary stochastic processes" , Moscow (1964) (In Russian) |
How to Cite This Entry:
Spectral semi-invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectral_semi-invariant&oldid=48762
This article was adapted from an original article by I.G. Zhurbenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article ,
,  , be a real stationary stochastic process for which
, be a real stationary stochastic process for which  . The semi-invariants (cf. Semi-invariant) of this process,
. The semi-invariants (cf. Semi-invariant) of this process,
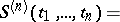
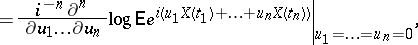
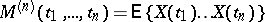
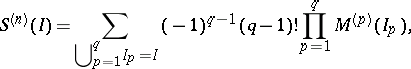
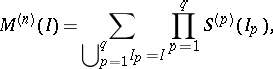

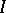 into disjoint subsets
into disjoint subsets  . It is said that
. It is said that  if, for all
if, for all 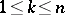 , there is a complex measure of bounded variation
, there is a complex measure of bounded variation 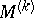 on
on  such that for all
such that for all  ,
,
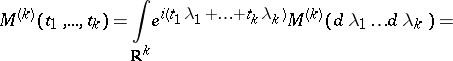

 , defined on a system of Borel sets, is called a spectral semi-invariant if, for all
, defined on a system of Borel sets, is called a spectral semi-invariant if, for all  ,
,
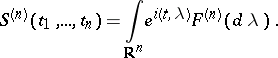
 exists and has bounded variation if
exists and has bounded variation if 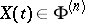 . In the case of a stationary process
. In the case of a stationary process 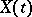 , the semi-invariants
, the semi-invariants  are invariant under translation:
are invariant under translation:

 and
and  are concentrated on the manifold
are concentrated on the manifold  . If the measure
. If the measure  is absolutely continuous with respect to Lebesgue measure on this manifold, then there is a spectral density
is absolutely continuous with respect to Lebesgue measure on this manifold, then there is a spectral density  of order
of order  , defined by the equations
, defined by the equations
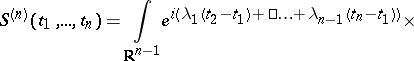
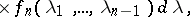
 . In the case of discrete time one must replace
. In the case of discrete time one must replace  in all formulas above by the
in all formulas above by the 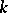 -dimensional cube
-dimensional cube  ,
,  .
.