Sonin integral
From Encyclopedia of Mathematics
The representation of a cylinder function (cf. Cylinder functions) by a contour integral
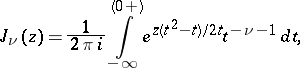 |
where  is arbitrary and
is arbitrary and 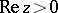 or
or 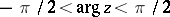 . Integrals of this type were studied by N.Ya. Sonin (1870).
. Integrals of this type were studied by N.Ya. Sonin (1870).
An integral of the form below is sometimes called a Sonin integral:
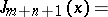 |
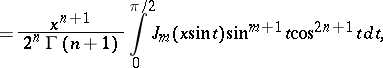 |
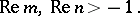 |
References
| [1] | M.A. Lavrent'ev, B.V. Shabat, "Methoden der komplexen Funktionentheorie" , Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian) |
| [2] | E. Jahnke, F. Emde, F. Lösch, "Tafeln höheren Funktionen" , Teubner (1966) |
Comments
In Western practice one usually writes Sonine integral. Transformed versions of the contour integral were independently obtained by L. Schläfli (1873) and integrals of this type are also called Schläfli integrals. The second mentioned integral is known as Sonine's first finite integral.
References
| [a1] | G.N. Watson, "The theory of Bessel functions" , 1 , Cambridge Univ. Press (1944) pp. Formulas 6.2(2), 12.11(1) |
How to Cite This Entry:
Sonin integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sonin_integral&oldid=48750
Sonin integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sonin_integral&oldid=48750
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article