Sommerfeld integral

An integral representation of the cylinder functions by a contour integral: The Hankel functions of the first kind are given by

where 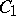is a curve from 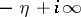to 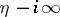, 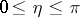; the Hankel functions of the second kind are given by

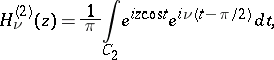where 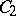is a curve from to 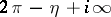, 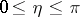; the Bessel functions of the first kind are given by

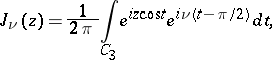where 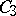is a curve from 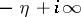to 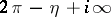, 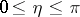. The representation is valid in the domain 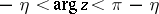, and is named after A. Sommerfeld [1].

References

[1]	A. Sommerfeld, "Mathematische Theorie der Diffraction" Math. Ann. , 47 (1896) pp. 317–374
[2]	E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German)
[3]	G.N. Watson, "A treatise on the theory of Bessel functions" , 1–2 , Cambridge Univ. Press (1952)

Comments

The Hankel functions are also called Bessel functions of the first kind.