Sokhotskii formulas
Formulas first discovered by Yu.V. Sokhotskii [1], expressing the boundary values of a Cauchy-type integral. With more complete proofs but significantly later, the formulas were obtained independently by J. Plemelj .
Let 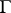 :
: 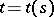 ,
, 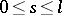 ,
, 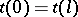 , be a closed smooth Jordan curve in the complex
, be a closed smooth Jordan curve in the complex  -plane, let
-plane, let  be the complex density in a Cauchy-type integral along
be the complex density in a Cauchy-type integral along 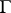 , on which
, on which 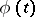 satisfies a Hölder condition:
satisfies a Hölder condition:
 |
let 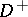 be the interior of
be the interior of 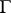 ,
, 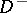 its exterior, and let
its exterior, and let
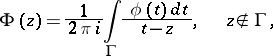 | (1) |
be a Cauchy-type integral. Then, for any point 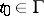 the limits
the limits
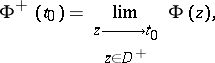 |
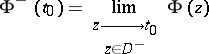 |
exist and are given by the Sokhotskii formulas
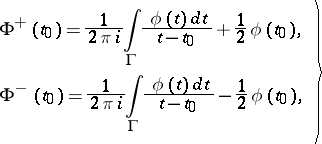 | (2) |
or, equivalently,
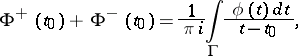 |
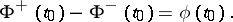 |
The integrals along 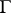 on the right-hand sides of these formulas are understood in the sense of the Cauchy principal value and are so-called singular integrals. By taking, under these conditions,
on the right-hand sides of these formulas are understood in the sense of the Cauchy principal value and are so-called singular integrals. By taking, under these conditions, 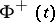 (or
(or 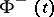 ) as values of the integral
) as values of the integral 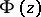 on
on 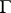 , one thus obtains a function
, one thus obtains a function  that is continuous in the closed domain
that is continuous in the closed domain 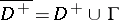 (respectively,
(respectively, 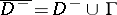 ). In the large,
). In the large, 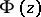 is sometimes described as a piecewise-analytic function.
is sometimes described as a piecewise-analytic function.
If  , then
, then 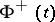 and
and 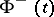 are also Hölder continuous on
are also Hölder continuous on 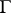 with the same exponent
with the same exponent 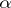 , while if
, while if 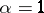 , with any exponent
, with any exponent 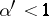 . For the corner points
. For the corner points 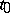 of a piecewise-smooth curve
of a piecewise-smooth curve  (see Fig.), the Sokhotskii formulas take the form
(see Fig.), the Sokhotskii formulas take the form
 | (3) |
In the case of a non-closed piecewise-smooth curve 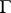 , the Sokhotskii formulas (2) and (3) remain valid for the interior points of the arc
, the Sokhotskii formulas (2) and (3) remain valid for the interior points of the arc 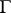 .
.
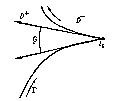
Figure: s086020a
The Sokhotskii formulas play a basic role in solving boundary value problems of function theory and in the theory of singular integral equations (see [3], [5]), and also in solving various applied problems in function theory (see [4]).
The question naturally arises as to the possibility of extending the conditions on the contour 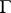 and the density
and the density 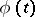 , in such a way that the Sokhotskii formulas (possibly with some restrictions) remain valid. The most significant results in this direction are due to V.V. Golubev and I.I. Privalov (see [6], [8]). For example, let
, in such a way that the Sokhotskii formulas (possibly with some restrictions) remain valid. The most significant results in this direction are due to V.V. Golubev and I.I. Privalov (see [6], [8]). For example, let 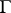 be a rectifiable Jordan curve, and let the density
be a rectifiable Jordan curve, and let the density 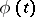 be, as before, Hölder continuous on
be, as before, Hölder continuous on 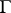 . Then the Sokhotskii formulas (2) hold almost everywhere on
. Then the Sokhotskii formulas (2) hold almost everywhere on 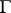 , where
, where 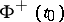 and
and 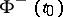 are understood as non-tangential boundary values of the Cauchy-type integral from inside and outside
are understood as non-tangential boundary values of the Cauchy-type integral from inside and outside  , respectively, but
, respectively, but 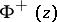 and
and 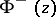 are, in general, not continuous in the closed domains
are, in general, not continuous in the closed domains 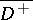 and
and 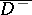 .
.
For spatial analogues of the Sokhotskii formulas see [7].
References
| [1] | Yu.V. Sokhotskii, "On definite integrals and functions used in series expansions" , St. Petersburg (1873) (In Russian) (Dissertation) |
| [2a] | J. Plemelj, "Ein Ergänzungssatz zur Cauchyschen Integraldarstellung analytischer Funktionen, Randwerte betreffend" Monatsh. Math. Phys. , 19 (1908) pp. 205–210 |
| [2b] | J. Plemelj, "Riemannsche Funktionenscharen mit gegebener Monodromiegruppe" Monatsh. Math. Phys. , 19 (1908) pp. 211–245 |
| [3] | N.I. Muskhelishvili, "Singular integral equations" , Wolters-Noordhoff (1972) (Translated from Russian) |
| [4] | N.I. Muskhelishvili, "Some basic problems of the mathematical theory of elasticity" , Noordhoff (1975) (Translated from Russian) |
| [5] | F.D. Gakhov, "Boundary value problems" , Pergamon (1966) (Translated from Russian) |
| [6] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [7] | A.V. Bitsadze, "Fundamentals of the theory of analytic functions of a complex variable" , Moscow (1972) (In Russian) |
| [8] | B.V. Khvedelidze, "The method of Cauchy-type integrals in the discontinuous boundary value problems of the theory of holomorphic functions of a complex variable" J. Soviet Math. , 7 (1977) pp. 309–415 Itogi Nauk. Sovremen. Probl. Mat. , 7 (1975) pp. 5–162 |
Comments
In the Western literature one usually speaks of the Plemelj formulas; the combination Sokhotskii–Plemelj formulas also occurs.
Much work has been done on Cauchy-type integrals in recent years. Thus, A.P. Calderón [a1] has proved the existence of non-tangential boundary values almost everywhere under weaker conditions, and he has studied the principal value integral, or Cauchy transform, in (2) as a bounded linear operator on appropriate  spaces. For further information see [a2].
spaces. For further information see [a2].
The idea of representing a function on a simple closed curve as the jump of an analytic function across that curve has been extensively generalized. Thus, every distribution on the unit circle and every tempered distribution on 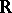 can be represented as such jumps in an appropriate sense, cf. [a3]. The ultimate in this direction are Sato's hyperfunctions (cf. [a5] and Hyperfunction).
can be represented as such jumps in an appropriate sense, cf. [a3]. The ultimate in this direction are Sato's hyperfunctions (cf. [a5] and Hyperfunction).
References
| [a1] | A.P. Calderón, "Cauchy integrals on Lipschitz curves and related operators" Proc. Nat. Acad. Sci. USA , 74 : 4 (1977) pp. 1324–1327 |
| [a2] | V.P. Khavin (ed.) S.V. Khrushchev (ed.) N.K. Nikol'skii (ed.) , Linear and complex analysis problem book , Lect. notes in math. , 1043 , Springer (1984) pp. Chapt. 6 (Translated from Russian) |
| [a3] | H.G. Tillmann, "Darstellung der Schwartzschen Distributionen durch analytischer Funktionen" Math. Z. , 77 (1961) pp. 106–124 |
| [a4] | M. Sato, "Theory of hyperfunctions I-II" J. Fac. Sci. Univ. Tokyo I , 8 (1959–1960) pp. 139–193; 387–437 |
| [a5] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983) |
Sokhotskii formulas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sokhotskii_formulas&oldid=48744