Smirnov  -samples test
-samples test
A non-parametric (or distribution-free) statistical test for testing hypotheses about the homogeneity of two samples.
Let 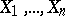 and
and 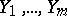 be mutually-independent random variables, where each sample consists of identically continuously distributed elements, and suppose one wishes to test the hypothesis
be mutually-independent random variables, where each sample consists of identically continuously distributed elements, and suppose one wishes to test the hypothesis 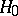 that both samples are taken from the same population. If
that both samples are taken from the same population. If
are the order statistics corresponding to the given samples, and 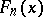 and
and 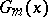 are the empirical distribution functions corresponding to them, then
are the empirical distribution functions corresponding to them, then 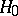 can be written in the form of the identity:
can be written in the form of the identity:
Further, consider the following hypotheses as possible alternatives to 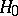 :
:
To test 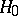 against the one-sided alternatives
against the one-sided alternatives 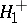 and
and 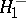 , and also against the two-sided
, and also against the two-sided 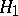 , N.V. Smirnov proposed a test based on the statistics
, N.V. Smirnov proposed a test based on the statistics
respectively, where it follows from the definitions of 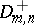 and
and  that under the hypothesis
that under the hypothesis 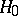 ,
, 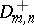 and
and 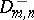 have the same distribution. Asymptotic tests can be based on the following theorem: If
have the same distribution. Asymptotic tests can be based on the following theorem: If 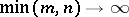 , then the validity of
, then the validity of 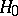 implies that
implies that
where 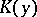 is the Kolmogorov distribution function (cf. Statistical estimator). Asymptotic expansions for the distribution functions of the statistics
is the Kolmogorov distribution function (cf. Statistical estimator). Asymptotic expansions for the distribution functions of the statistics 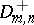 and
and  have been found (see [4]–[6]).
have been found (see [4]–[6]).
Using the Smirnov test with significance level 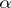 ,
,  may be rejected in favour of one of the above alternatives
may be rejected in favour of one of the above alternatives 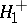 ,
, 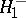 when the corresponding statistic exceeds the
when the corresponding statistic exceeds the 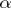 -critical value of the test; this value can be calculated using the approximations obtained by L.N. Bol'shev [2] by means of Pearson asymptotic transformations.
-critical value of the test; this value can be calculated using the approximations obtained by L.N. Bol'shev [2] by means of Pearson asymptotic transformations.
See also Kolmogorov test; Kolmogorov–Smirnov test.
References
| [1] | N.V. Smirnov, "Estimates of the divergence between empirical distribution curves in two independent samples" Byull. Moskov. Gosudarstv. Univ. (A) , 2 : 2 (1939) pp. 3–14 |
| [2] | L.N. Bol'shev, "Asymptotically Pearson transformations" Theor. Probab. Appl. , 8 (1963) pp. 121–146 Teor. Veroyatnost. i Primenen. , 8 : 2 (1963) pp. 129–155 |
| [3] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [4] | V.S. Korolyuk, "Asymptotic analysis of the distribution of the maximum deviation in the Bernoulli scheme" Theor. Probab. Appl. , 4 (1959) pp. 339–366 Teor. Veroyatnost. i Primenen. , 4 (1959) pp. 369–397 |
| [5] | Li-Chien Chang, "On the exact distribution of A.N. Kolmogorov's statistic and its asymptotic expansion (I and II)" Matematika , 4 : 2 (1960) pp. 135–139 (In Russian) |
| [6] | A.A. Borovkov, "On the two-sample problem" Izv. Akad. Nauk SSSR Ser. Mat. , 26 : 4 (1962) pp. 605–624 (In Russian) |
References
| [a1] | D.B. Owen, "A handbook of statistical tables" , Addison-Wesley (1962) |
| [a2] | E.S. Pearson, H.O. Hartley, "Biometrika tables for statisticians" , 2 , Cambridge Univ. Press (1972) |
How to Cite This Entry:
Smirnov test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Smirnov_test&oldid=48739
This article was adapted from an original article by M.S. Nikulin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article -samples test
-samples test
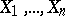 and
and 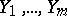 be mutually-independent random variables, where each sample consists of identically continuously distributed elements, and suppose one wishes to test the hypothesis
be mutually-independent random variables, where each sample consists of identically continuously distributed elements, and suppose one wishes to test the hypothesis 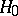 that both samples are taken from the same population. If
that both samples are taken from the same population. If
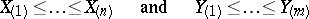
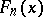 and
and 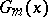 are the empirical distribution functions corresponding to them, then
are the empirical distribution functions corresponding to them, then 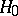 can be written in the form of the identity:
can be written in the form of the identity:
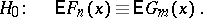
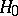 :
:
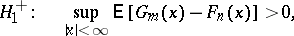
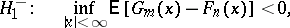
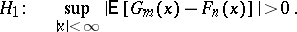
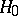 against the one-sided alternatives
against the one-sided alternatives 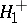 and
and 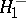 , and also against the two-sided
, and also against the two-sided 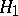 , N.V. Smirnov proposed a test based on the statistics
, N.V. Smirnov proposed a test based on the statistics
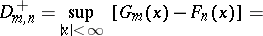
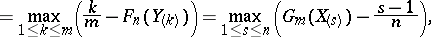
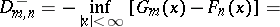
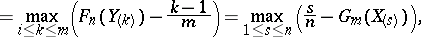
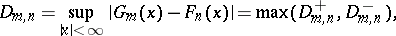
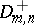 and
and  that under the hypothesis
that under the hypothesis 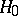 ,
, 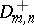 and
and 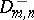 have the same distribution. Asymptotic tests can be based on the following theorem: If
have the same distribution. Asymptotic tests can be based on the following theorem: If 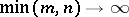 , then the validity of
, then the validity of 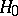 implies that
implies that
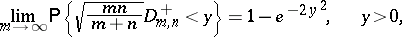
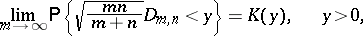
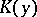 is the Kolmogorov distribution function (cf. Statistical estimator). Asymptotic expansions for the distribution functions of the statistics
is the Kolmogorov distribution function (cf. Statistical estimator). Asymptotic expansions for the distribution functions of the statistics 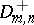 and
and  have been found (see [4]–[6]).
have been found (see [4]–[6]).
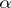 ,
,  may be rejected in favour of one of the above alternatives
may be rejected in favour of one of the above alternatives 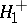 ,
, 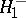 when the corresponding statistic exceeds the
when the corresponding statistic exceeds the 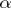 -critical value of the test; this value can be calculated using the approximations obtained by L.N. Bol'shev [2] by means of Pearson asymptotic transformations.
-critical value of the test; this value can be calculated using the approximations obtained by L.N. Bol'shev [2] by means of Pearson asymptotic transformations.