Small object
A concept which singles out objects in a category that have intrinsically the properties of a mathematical structure with a finite number of generators (finite-dimensional linear space, finitely-generated group, etc.). Let 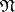 be a category with coproducts. An object
be a category with coproducts. An object 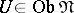 is called small if for any morphism
is called small if for any morphism
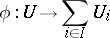 |
where 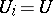 ,
, 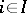 , and
, and  is the imbedding of the
is the imbedding of the 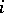 -th summand in the coproduct, there is a finite subset of the indices
-th summand in the coproduct, there is a finite subset of the indices 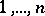 such that
such that 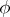 factors through the morphism
factors through the morphism
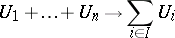 |
induced by  . Sometimes a stronger definition is given in which it is not assumed that all summands in the coproduct
. Sometimes a stronger definition is given in which it is not assumed that all summands in the coproduct 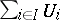 coincide with
coincide with 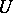 .
.
In varieties of finitary universal algebras the following conditions on an algebra 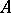 are equivalent: a)
are equivalent: a) 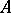 is a small object of the category; b)
is a small object of the category; b) 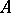 has a finite number of generators; and c) the covariant hom-functor
has a finite number of generators; and c) the covariant hom-functor 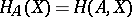 commutes with colimits (direct limits) of directed families of monomorphisms. Property c) is often taken as the definition of a finitely-generated object of an arbitrary category.
commutes with colimits (direct limits) of directed families of monomorphisms. Property c) is often taken as the definition of a finitely-generated object of an arbitrary category.
Comments
In an additive category, an object 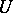 is small if and only if the Abelian-group-valued functor
is small if and only if the Abelian-group-valued functor 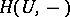 preserves coproducts. Some authors take this as the definition of smallness in non-additive categories: it produces a more restrictive condition than the one above, equivalent to the requirement that every morphism from
preserves coproducts. Some authors take this as the definition of smallness in non-additive categories: it produces a more restrictive condition than the one above, equivalent to the requirement that every morphism from 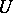 to a coproduct should factor through a unique summand. In practice the term is rarely used outside the context of additive categories.
to a coproduct should factor through a unique summand. In practice the term is rarely used outside the context of additive categories.
Small object. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Small_object&oldid=48736