Skew-symmetric tensor

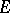A tensor over an -dimensional vector space that is invariant under the operation of alternation with respect to some group of its indices. The components of a skew-symmetric tensor are skew-symmetric with respect to the corresponding group of indices, i.e. if two indices are exchanged the components change sign (in the sense of the additive law of the field 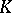over which 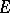is defined), and if two indices are equal the components vanish.

The most important skew-symmetric tensors are those that remain invariant under alternation with respect to the entire group of covariant or contravariant indices. A contravariant (covariant) skew-symmetric tensor of valency is an -vector or multi-vector over 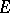(respectively, over 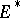, the space dual to 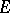); they are elements of the exterior algebra of the vector space 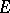. The exterior algebra over 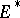is usually called the algebra of exterior forms, identifying covariant skew-symmetric tensors of valency with -forms.

For references see Exterior algebra.