Singular point, index of a

One of the basic characteristics of an isolated singular point of a vector field. Let a vector field be defined on 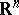, and let 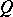be a sphere of small radius surrounding a singular point 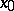such that . The degree of the mapping (cf. Degree of a mapping)

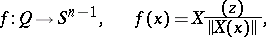is then called the index, 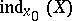, of the singular point 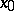of the vector field , i.e.

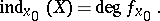If 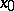is non-degenerate, then

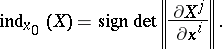Comments

See also Poincaré theorem; Rotation of a vector field.

References

[a1]	M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French)
[a2]	J.A. Thorpe, "Elementary topics in differential geometry" , Springer (1979)
[a3]	C. Conley, E. Zehnder, "Morse type index theory for flows and periodic solutions of Hamiltonian equations" Comm. Pure Appl. Math. , 37 (1984) pp. 207–253
[a4]	K.P. Rybakovskii, "The homotopy index and partial differential equations" , Springer (1987) (Translated from Russian)