Simson straight line

The straight line joining the feet of the perpendiculars from an arbitrary point 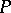of the circumscribed circle of a triangle onto its sides. It bisects the segment joining 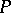to the point of intersection of the altitudes of the triangle. The Simson line is named after R. Simson, although its discovery predates him.

Comments

In the work of Simson (1687–1768) there is no mention of this line. It was really discovered by W. Wallace in 1799 (see, e.g., [a1], Chapt. V and p. 300; [a2], p. 16; [a3]).

References

[a1]	N. Altshiller-Court, "College geometry" , New York (1952)
[a2]	H.S.M. Coxeter, "Introduction to geometry" , Wiley (1989)
[a3]	C.G. Gillispie, Dictionary of scientific biography , 14 (1976) pp. 140
[a4]	M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French)
[a5]	J.L. Coolidge, "A treatise on the circle and the sphere" , Chelsea, reprint (1971)