Similar statistic

A statistic having a fixed probability distribution under some compound hypothesis.

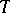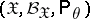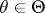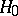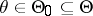Let the statistic map the sample space , , into a measurable space and consider some compound hypothesis : . In that case, if for any event 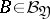the probability

(*)

one says that is a similar statistic with respect to 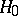, or simply that it is a similar statistic. It is clear that condition (*) is equivalent to saying that the distribution of the statistic 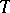does not vary when 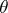runs through 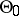. With this property in view, it is frequently said of a similar statistic that it is independent of the parameter 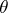, . Similar statistics play a large role in constructing similar tests, and also in solving statistical problems with nuisance parameters.

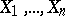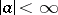Example 1. Let be independent random variables with identical normal distribution with and 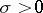. Then for any 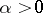the statistic

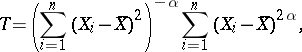where

is independent of the two-dimensional parameter .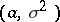

Example 2. Let 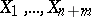be independent identically-distributed random variables whose distribution functions belong to the family of all continuous distribution functions on . If and 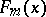are empirical distribution functions constructed from the observations 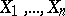and 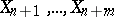, respectively, then the Smirnov statistic

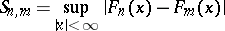is similar with respect to the family .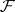

References

[1]	J.-L. Soler, "Basic structures in mathematical statistics" , Moscow (1972) (In Russian; translated from French)
[2]	Yu.V. Linnik, "Statistical problems with nuisance parameters" , Amer. Math. Soc. (1968) (Translated from Russian)
[3]	J.-R. Barra, "Mathematical bases of statistics" , Acad. Press (1981) (Translated from French)

References

[a1]	E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986)