Similar operators
From Encyclopedia of Mathematics
Operators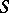 
and 
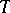(not necessarily bounded) on a Banach space 
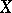for which there exists a bounded operator 
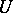on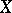 
having a bounded inverse and such that the following relation applies:
 |
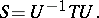If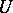 
is a unitary operator, then 
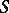and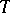 
are said to be unitarily equivalent.
This concept is an example of the concept of similar mappings. Let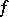 
and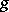 
be two mappings of a set 
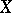into itself. If there is a bijection 
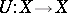such that 
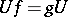, then these mappings are said to be similar. Attempts have been made to give a definition of similarity for mappings from one set 
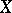into another 
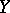; for example, such mappings are called similar if there exist bijections 
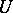and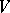 
of the sets 
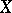and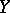 
into themselves such that 
.
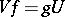How to Cite This Entry:
Similar operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Similar_operators&oldid=48699
Similar operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Similar_operators&oldid=48699
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article