Significant figure
significant digit
A term pertaining to the approximate specification of a real number. Let a real number  be represented in a number system with base
be represented in a number system with base 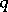 by a
by a 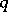 -ary fraction
-ary fraction
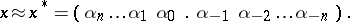 |
In this notation, suppose that 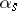 is the first non-zero digit, counted from the left. Then all subsequent digits are called significant digits of the approximate number
is the first non-zero digit, counted from the left. Then all subsequent digits are called significant digits of the approximate number 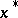 .
.
A significant digit 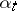 is said to be correct if the absolute error
is said to be correct if the absolute error 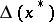 of
of 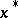 , i.e. the difference
, i.e. the difference 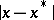 , satisfies the inequality
, satisfies the inequality
 |
In approximate specification of a real number it is usually meaningful to specify only significant digits.
Comments
One speaks of doing a calculation to three significant digits if each calculated result is rounded so that there are no more than three digits after and including the first non-zero digit. One says that an approximate number resulting from a calculation (in mathematics) or from a measurement (in sciences and technology) 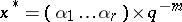 with
with  significant digits is correct to
significant digits is correct to  significant digits,
significant digits, 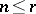 , if the error
, if the error
 |
is less than 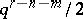 . Usually
. Usually 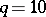 or
or  . For example,
. For example,  is the correct answer to three significant digits of
is the correct answer to three significant digits of 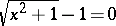 .
.
References
| [a1] | D.M. Young, R.T. Gregory, "A survey of numerical mathematics" , I , Dover, reprint (1988) pp. Chapt. 1 |
Significant figure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Significant_figure&oldid=48697